2015-10-13
901
Этот критерий является алгебраическим. В форме, предложенной Гурвицем (1895), из коэффициентов характеристического уравнения (5-4) составляется квадратная матрица (таблица) Гурвица, имеющая N столбцов и строк,
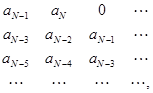
правило построения которой очевидно. Отсутствующие коэффициенты заменяются нулями.
Для устойчивости системы необходимо и достаточно, чтобы все главные диагональные миноры Δ n матрицы (определители Гурвица) были положительны:
, 
, …, 
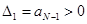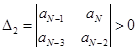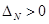(5-9)
Вычисление определителей Гурвица довольно трудоемко при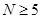 
. В этом случае удобнее форма Рауса (1875), для чего составляется таблица Рауса, имеющая N+ 1строку, правило построения которой очевидно из примера. Коэффициентам сотрицательными индексами соответствуют нули.
 |  |  | … | |
 |  |  | … | |
 |  |  |  | … |
 |  |  |  | … |
| … | … | … | … | … |
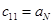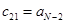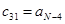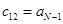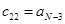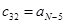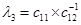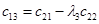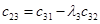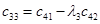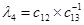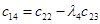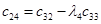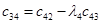Для устойчивости системы необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны
, 
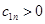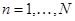. (5-10)
Если система неустойчива, то число перемен знаков в первом столбце равно числу правых корней характеристического уравнения.
Критерий Рауса — Гурвица удобен для определения предельных значений параметров САР, при которых система находится на границе устойчивости. Эти значения находятся либо из условий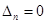 
, либо 
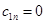. Заметим, что в (5-9)
,
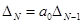поэтому при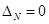 
система находится либо на границе апериодической устойчивости (
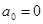), когда один из корней характеристического уравнения равен нулю, либо на границе колебательной устойчивости (
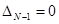), когда два сопряженных корня находятся на мнимой оси.
Пример 5-1 [1]. Рассмотрим условия устойчивости статической САР скорости двигателя. Передаточная функция разомкнутой системы равна
,
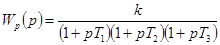где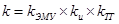 
— статический коэффициент усиления. Характеристическое уравнение (5-8) замкнутой системы в данном случае имеет вид
,
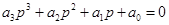где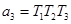 
, 
, 
,
.
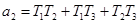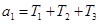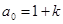Определители Гурвица равны
,
,
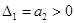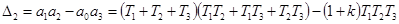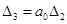
Найдем предельный коэффициент k. Из условия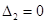 
получаем предельное значение k, при котором система находится на границе колебательной устойчивости,
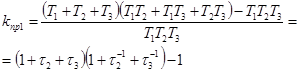(5-11)
где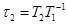 
, 
.
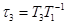Из условия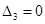 
, т. е. 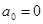находим другое предельное значение 
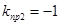(отрицательное и соответствует положительной обратной связи), при котором система находится на границе апериодической устойчивости. Анализируя полученный результат, приходим к выводу, что САР устойчива при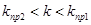 
Из (5-11) следует, что предельный коэффициент усиления системы определяется лишь соотношением постоянных, времени. Заметим, что при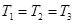 
, получаем минимальное значение 
.
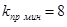На практике стремятся получить системы с весьма большими предельными коэффициентами усиления. Это объясняется желанием иметь у системы большой коэффициент усиления, что приводит, как увидим далее, к повышению точности регулирования. Поскольку, увеличивать коэффициент можно только до предельного, то и стремятся увеличить последний. Для такого увеличения, как следует из (5-11), нужно «раздвигать» постоянные времени. Например, при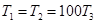 
получаем 
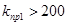. Однако этот путь практически нереален. Дело в том, что при конструировании аппаратуры стремятся уменьшить постоянные времени, и поэтому их дальнейшее уменьшение почти невозможно. Вполне возможно увеличить постоянные времени (например, для увеличения постоянной времени двигателя надо насадить на его ось массивный маховик, что приведет к увеличению момента инерции и, как следует из (3-9), к увеличению постоянной времени), однако это приведет к снижению быстродействия системы, что нежелательно. Наиболее общий путь увеличения предельного коэффициента усиления состоит в изменении структурной схемы САР (коррекции) путем введения дополнительных звеньев и контуров. Этот путь будет рассмотрен далее в гл. 7.
