ТЕСТОВЫЕ ЗАДАНИЯ.
| № № | ответы | № № | ответы | № № | ответы | № № | ответы | № № | ответы |
| 1. | 11. | 21. | 31. | 41. | |||||
| 2. | 12. | 22. | 32. | 42. | |||||
| 3. | 13. | 23. | 33. | 43. | |||||
| 4. | 14. | 24. | 34. | 44. | |||||
| 5. | 15. | 25. | 35. | 45. | |||||
| 6. | 16. | 26. | 36. | 46. | |||||
| 7. | 17. | 27. | 37. | 47. | |||||
| 8. | 18. | 28. | 38. | 48. | |||||
| 9. | 19. | 29. | 39. | 49. | |||||
| 10. | 20. | 30. | 40. | 50. |
1. 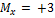 .; 2.
.; 2. 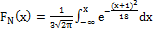 ; 3.
; 3. 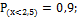 4.
4. 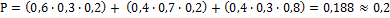 ; 5.
; 5. 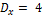 ; 6.
; 6. 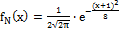 ; 7.
; 7. 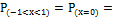 0,1; 8.
0,1; 8. 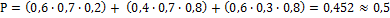 ; 9. C = 8; 10. Указание: при построении графиков необходимо учесть общий характер функции распределения вероятностей и тот факт, что стандартное отклонение определяет тангенс угла наклона графика функции распределения вероятностей в точке соответствующей математическому ожиданию.;
; 9. C = 8; 10. Указание: при построении графиков необходимо учесть общий характер функции распределения вероятностей и тот факт, что стандартное отклонение определяет тангенс угла наклона графика функции распределения вероятностей в точке соответствующей математическому ожиданию.;
11.
| F(x) | 0,00 | при x ≤ -2 | 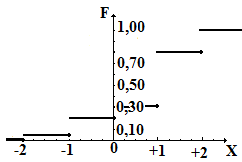 |
| 0,05 | при -2 < x ≤ -1 | ||
| 0, 20 | при -1 < x ≤ 0 | ||
| 0,30 | при -0 < x ≤ +1 | ||
| 0,80 | при +1 < x ≤ +2 | ||
| 1,00 | при x > +2 |
12. 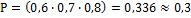 ;13.
;13. 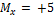 ; 14.
; 14. 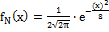 ; 15.
; 15. 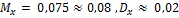 ; 16.
; 16. 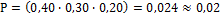 ;
;
17. Математическое ожидание М(х) случайной величины Х (отклонение диаметра шарика от проектного размера) М(х) = 0. Стандартное отклонение σ = 0,4 задано по условию задачи. Тогда: 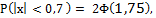 где
где 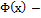 функция Лапласа. По таблице (см. Справочные материалы №4) находим:
функция Лапласа. По таблице (см. Справочные материалы №4) находим:
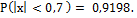 Следуя классическому определению вероятности:
Следуя классическому определению вероятности: 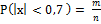 ,
, 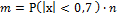 . Для n = 100 и
. Для n = 100 и 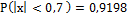 получаем m=91,98 ≈ 92.
получаем m=91,98 ≈ 92.
18. 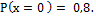 19.
19. 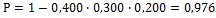 . 20.
. 20. 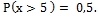
21. 1). Событие А - сигнальная лампочка прибора с перегорает при включении в сеть. 2). Найдём вероятность события противоположного событию А. Р(«не А») = 1 – Р(А) = 1 – 0,1 = 0,9. 3). Событие «лампочка не перегорает при первом включении» и событие «лампочка перегорает при втором включении» являются независимыми. Можно применить формулу умножения вероятностей для независимых событий. 4). Р(А×В) =Р(А) × Р(В). 5). Искомая вероятность Р = 0,9 × 0,1 = 0, 09
22. 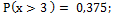 23. М(х) = 0,1; 24.
23. М(х) = 0,1; 24. 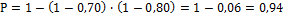 ; 25. М(х) = 0;
; 25. М(х) = 0;
26. 1). Пусть случайным событием А является рождение мальчика. 2). Согласно статистическому определению вероятности: Р(А) = 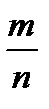 , где m - число рождений мальчиков, n - суммарное число рождений мальчиков и девочек. 3). Событие – «рождение девочки» является противоположным событию А.
, где m - число рождений мальчиков, n - суммарное число рождений мальчиков и девочек. 3). Событие – «рождение девочки» является противоположным событию А. 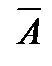 - случайное событие - рождение девочки. 4). Вспомнив аксиому сложения вероятностей:
- случайное событие - рождение девочки. 4). Вспомнив аксиому сложения вероятностей: 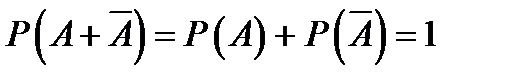 5).Найдём вероятность рождения девочки
5).Найдём вероятность рождения девочки 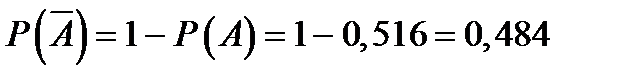
27. 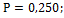 28.
28. 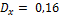 ; 29.
; 29. 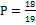 ; 30.
; 30. 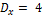 ;
;
31. 1). В данном случае надежность системы представляет событие – «хотя бы один блок работает». 2). Событие противоположное событию – «хотя бы один блок работает» Это - «Ни один из блоков не работает». 3). События образуют полную группу попарно несовместных событий.
4). Применяя формулу сложения вероятностей для случая полной группы попарно несовместных событий: 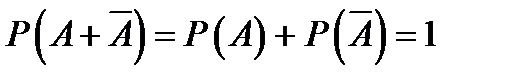 . 5). Надёжность системы:
. 5). Надёжность системы: 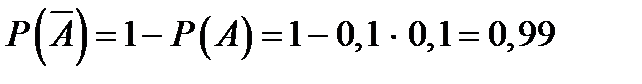
32. 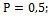 33.
33. 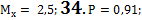 35.
35. 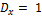 ;
;
36. 1). Событие А - событие, состоящее в том, что после 3 игр в коробке не останется не игранных мячей. 2). А = А1 × А2 × А3, где А1 – событие, состоящее в то, что для первой игры взяты три не игранных мяча. А2 - событие, состоящее в то, что для второй игры взяты три не игранных мяча. А3 - событие, состоящее в то, что для третьей игры взяты три не игранных мяча. 3). А1 - событие, равное произведению трёх событий В1 , В2 и В3. В1 - событие «первый мяч для первой игры оказался не игранным», В2 - событие «второй мяч для первой игры оказался не игранным» и В3 - событие «третий мяч для первой игры оказался не игранным».4). Р(А1) = (9/9) ×(8/8)×(7/7); Р(А2) = (6/9) ×(5/8)×(4/7); Р(А3) = (3/9) ×(2/8)×(1/7). 5). По формуле умножения вероятностей для зависимых событий Р(А) = Р(А1) × Р(А2) × Р(А3) = (9/9) × (8/8) ×(7/7) × (6/9) ×(5/8) × (4/7) × (3/9) ×(2/8)×(1/7)» 0,003
37. 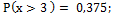 38.
38. 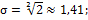 39.
39. 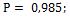 40.
40. 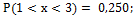 41.
41. 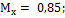
42. 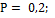 43.
43. 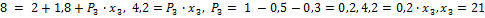 ; 44.
; 44. 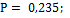 45.
45. 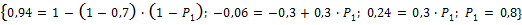 ; 46. Указание: см. задачу 11 ;47.
; 46. Указание: см. задачу 11 ;47. 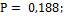 48.
48. 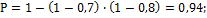
49. 1). Уясним, что речь идет о случайной величине, распределенной по нормальному закону с известным математическим ожиданием и неизвестной дисперсией.
2). Схематически изобразим её график
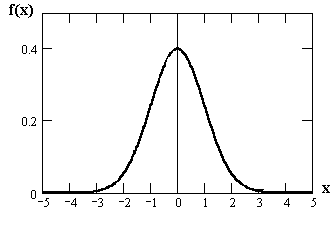
3). Воспользуемся свойствами симметрии графика. Вертикаль, проходящая через математическое ожидание, делит весь график функции на две равные части.
4). Геометрически определённый интеграл представляет площадь под кривой плотности распределения вероятностей
5). По условиям нормировки непрерывной случайной величины вся площадь под кривой равна единице. Половина площади под кривой равна 0,5.
50. 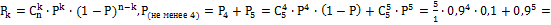 0,92; 51.
0,92; 51. 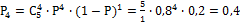 ; 52. (6,87; 7,73);
; 52. (6,87; 7,73);
53. Закон распределения Пуассона можно записать в виде следующей таблицы:
| X | … | k | … | |||
| P | 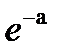 | 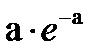 | 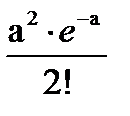 | … | 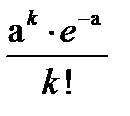 | … |
a – средняя по ансамблю (мат.ожидание, дисперсия). P(0) = e-a, 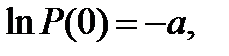 что и обеспечивает нам знание среднего по ансамблю (в данном случае среднее число клеток в квадратном участке решётки). Р(0) =75/900 ≈ 0,0833, -lnP(0) ≈ -ln(0,0833) ≈ 2,485. Общеечисло имеющихся клеток можно оценить: N ≈ 2,485× 900 ≈ 2236.
что и обеспечивает нам знание среднего по ансамблю (в данном случае среднее число клеток в квадратном участке решётки). Р(0) =75/900 ≈ 0,0833, -lnP(0) ≈ -ln(0,0833) ≈ 2,485. Общеечисло имеющихся клеток можно оценить: N ≈ 2,485× 900 ≈ 2236.
54. 4; 55. 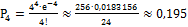 ; 56.
; 56. 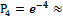 0,018; 57. 3500∙
0,018; 57. 3500∙ 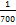 = 5; 58.
= 5; 58. 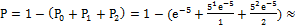 1-(1+5+12,5)
1-(1+5+12,5) 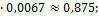 59.
59. 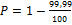 = 1-0,9999 = 0,0001, n = 0,0001
= 1-0,9999 = 0,0001, n = 0,0001 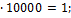 60.
60. 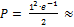 0,184;
0,184;
61. Пусть случайная величинаX – число болезнетворных микробов, находящихся в 2 дм3 воздуха. Примем гипотезу о пуассоновском распределении числа микробов, которые могут быть обнаружены в этом объёме. Математическое ожидание X равно:а = 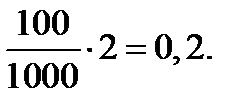 Вероятность, что в данном объёме будет обнаружен хотя бы один микроб, равна
Вероятность, что в данном объёме будет обнаружен хотя бы один микроб, равна 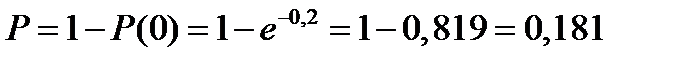 .
.
62. Обозначим событие: С – абоненту придётся набрать номер не более, чем три раза.
Это событие состоит в том, что абоненту придётся набрать номер или один, или два или три раза. Рассмотрим следующие события:
С1 – абонент будет набирать номер один раз;
С2 - абонент будет набирать номер два раза;
С3 - абонент будет набирать номер три раза;
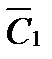 - в первый раз не набрана нужная цифра;
- в первый раз не набрана нужная цифра;
А - во второй раз набрана нужная цифра;
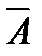 - во второй раз не набрана нужная цифра;
- во второй раз не набрана нужная цифра;
В – в третий раз набрана нужная цифра.
Событие С представляет собой сумму несовместных событий С1,С2 и С3: С = С1+С2 + С3.Вероятность события С1 равна 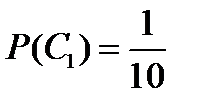 .
.
Событие С2 состоит в том, что в первый раз нужная цифра не набрана, а во второй - набрана. Это означает, что С2 представляет произведение событий 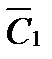 и А: С2 =
и А: С2 = 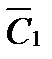 ∙ А. Вероятность события
∙ А. Вероятность события 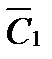 равна
равна 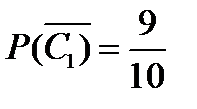 . Событие А является зависимым от события
. Событие А является зависимым от события 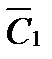 ; условная вероятность
; условная вероятность 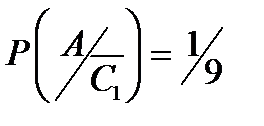 . Вероятность события С2 найдём по теореме умножения вероятностей зависимых событий.
. Вероятность события С2 найдём по теореме умножения вероятностей зависимых событий. 
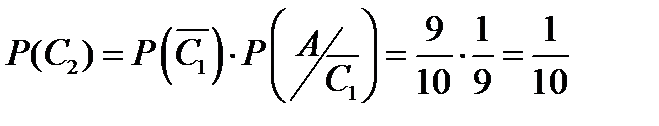 .
.
Событие С3 состоит в том, что и в первый, и во второй раз нужная цифра не набрана, а в третий раз – набрана. Это означает, что С3 представляет собой произведение зависимых событий 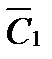 ,
, 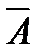 и В: С3 =
и В: С3 = 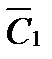 ∙
∙ 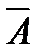 ∙ В. Условная вероятность
∙ В. Условная вероятность 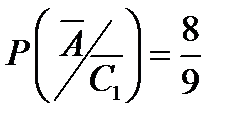 ; условная вероятность
; условная вероятность 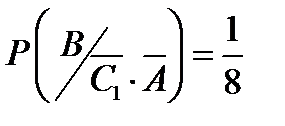 . Вероятность наступления события С3 найдём по теореме умножения вероятностей зависимых событий.
. Вероятность наступления события С3 найдём по теореме умножения вероятностей зависимых событий. 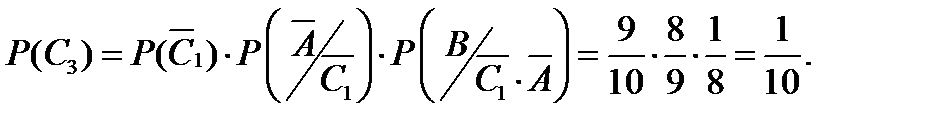
Искомую вероятность события С найдём по теореме сложения вероятностей несовместных событий. 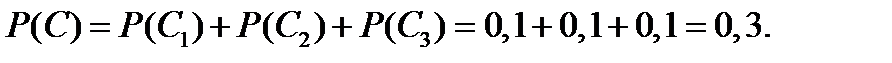
63. 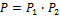 =
= 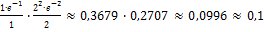 ; 64.
; 64. 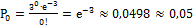 ; 65. P=1-(
; 65. P=1-(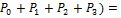 1 – (
1 – (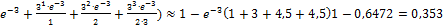 ; 66.
; 66. 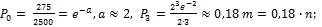 67.
67. 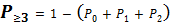 = 1 – (
= 1 – (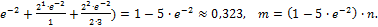
68. Фаг Т2 размер 200нм, длина волны видимого света (760-380 нм) больше размера фага, рассеяния нет, раствор прозрачный. Бактерия кишечной палочки – много больше, взвесьбактерий интенсивно рассеивает свет (пробирка с бактериями выглядит мутной). Предположим, что процесс взаимодействия вирусов с бактериями описывается распределением Пуассона.Закон распределения Пуассона можно записать в виде следующей таблицы:
| X | … | k | … | |||
| P | 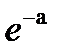 | 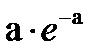 | 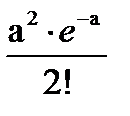 | … | 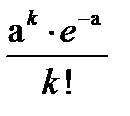 | … |
a – средняя по ансамблю. P(0) = e-a 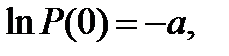 что и обеспечивает нам знание среднего по ансамблю.
что и обеспечивает нам знание среднего по ансамблю.
Хотя бы один вирус попал в клетку P(1), P(2) ……. P(0) – клетка не заражена.В 38 пробирок оставшихся мутными вирусы не попали.
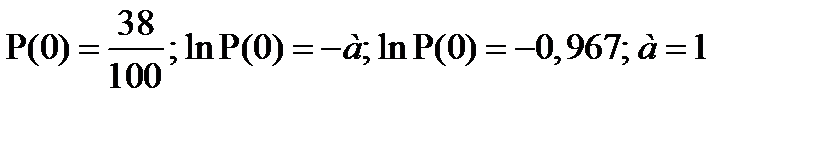
69.  =
= 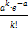 ,
, 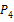 =
= 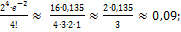 70. P=1-(
70. P=1-(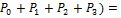 1 – (
1 – (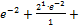
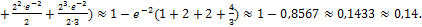 71.
71. 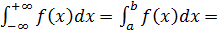 1,
1, 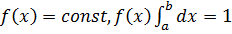 ,
, 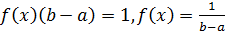 .
.
72. 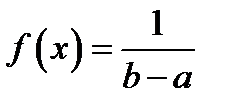 ,
, 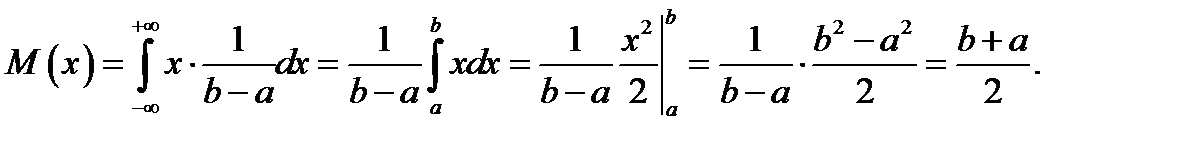
73. 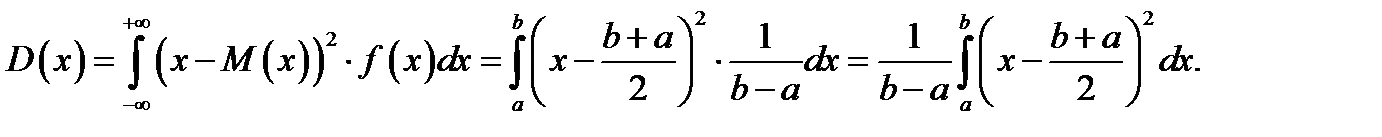

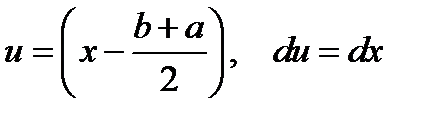
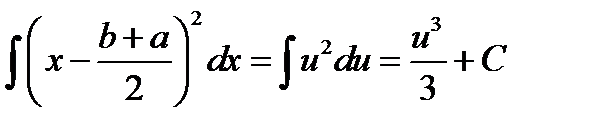
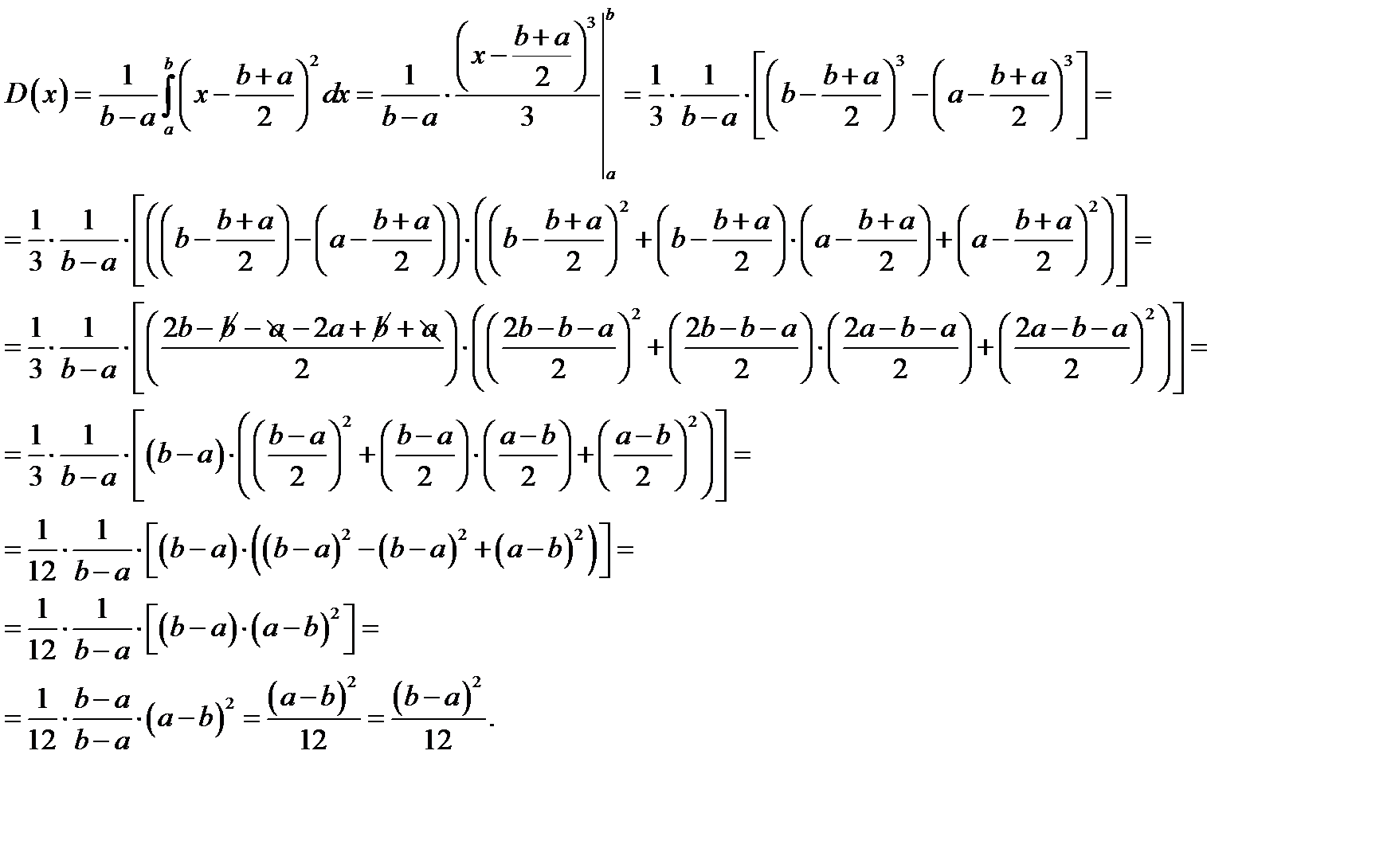
| 74. Дано: n = 20 m = 15 p = 0,05 Найти: P(A) -? | Решение: Сделаем допущение: «вероятность заразится гриппом от пациента не зависит от того сколько заразных пациентов осмотрел врач перед этим» (p = 0,05). В таком случае интересующее нас событие A состоит в совместном появлении более простых событий |
с равными вероятностями q =1- p = 1 - 0,05 = 0,95 в результате «опыта» — приёма записавшихся к врачу пациентов. Итак: 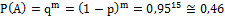 .
.
Ответ: 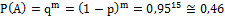 .
.
 2015-10-13
2015-10-13 1631
1631








