Механическая система состоит из прямоугольной вертикальной плиты 1 массой m1 =18 кг, движущейся вдоль горизонтальных направляющих, и груза D массой m2 =6 кг (рис. Д5.0–Д5.9, табл. Д5). В момент времени t0 =0, когда скорость плиты и0= 2 м/с, груз под действием внутренних сил начинает двигаться по желобу плиты. На рис. 0–3 желоб КЕ прямолинейный и при движении груза расстояние s = AD изменяется по закону 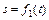 , а на рис. 4–9 желоб – окружность радиуса R =0,8 м и при движении груза угол
, а на рис. 4–9 желоб – окружность радиуса R =0,8 м и при движении груза угол 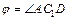 изменяется по закону
изменяется по закону 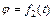 . В табл. Д5 эти зависимости даны отдельно для рис. 0 и 1, для рис. 2 и 3 и т. д., где s выражено в метрах, φ – в радианах, t – в секундах.
. В табл. Д5 эти зависимости даны отдельно для рис. 0 и 1, для рис. 2 и 3 и т. д., где s выражено в метрах, φ – в радианах, t – в секундах.
Считая груз материальной точкой и пренебрегая всеми сопротивлениями, определить величину, указанную в таблице в столбце «Найти», где обозначено: x1 – перемещение плиты за время от t0 =0 до t1 =1 с; и,, a,, Nt –значения в момент времени t1 =l с скорости плиты, ускорения плиты и полной нормальной реакции направляющих соответственно.
Указания. Задача Д5 на применение теорем о движении центра масс и об изменении количества движения системы. Первой теоремой удобнее пользоваться, когда надо найти перемещение (или закон движения) одного из тел системы, движущегося поступательно, а второй – когда надо найти скорость такого тела. При определении ускорения тела или реакции связи тоже удобнее воспользоваться первой теоремой.
Таблица Д5
| Номер условия | 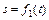 | 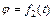 | Найти | |||
| рис. 0,1 | рис. 2,3 | рис. 4,5 | рис. 6,7 | рис. 8,9 | ||
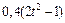 | 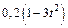 | 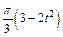 | 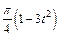 | 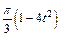 | x1 | |
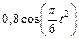 | 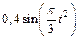 | 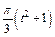 | 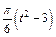 | 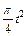 | u1 | |
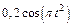 | 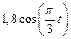 | 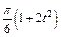 | 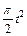 | 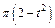 | a1 | |
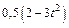 | 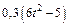 | 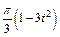 | 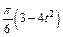 | 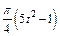 | x1 | |
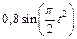 | 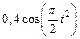 | 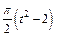 | 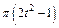 | 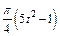 | N1 | |
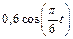 | 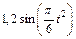 | 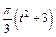 | 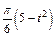 | 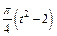 | u1 | |
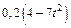 | 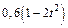 | 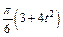 | 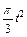 | 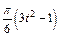 | x1 | |
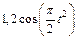 | 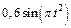 | 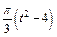 | 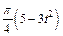 | 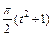 | a1 | |
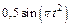 | 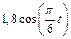 | 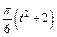 | 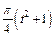 | 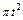 | N1 | |
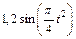 | 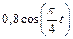 | 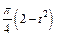 | 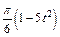 | 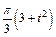 | u1 |
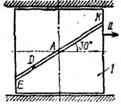 Рис. Д5.0 Рис. Д5.0 | 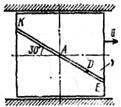 Рис. Д5.1 Рис. Д5.1 | ||
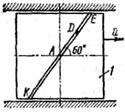 Рис. Д5.2 Рис. Д5.2 | 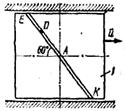 Рис. Д5.3 Рис. Д5.3 | 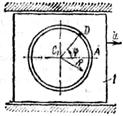 Рис. Д5.4 Рис. Д5.4 | |
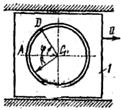 Рис. Д5.5 Рис. Д5.5 | 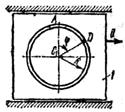 Рис. Д5.6 Рис. Д5.6 | 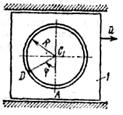 Рис. Д5.7 Рис. Д5.7 | |
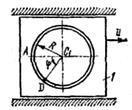 Рис. Д5.8 Рис. Д5.8 | 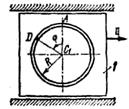 Рис. Д5.9 Рис. Д5.9 | ||
Пример Д5. В центре тяжести А тележки массой m1, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стержень AD длиной l с грузом D массой т2 на конце (рис. Д5, а),
В момент времени t0 =0, когда скорость тележки и0, стержень AD начинает вращаться вокруг оси А по закону 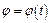 .
.
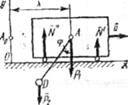
Рис. Д5а
Дано: m1 = 24 кг, m2 =12 кг, u0 =0,5 м/с, l =0,6 м, 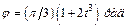 (t – в секундах).
(t – в секундах).
Определить в момент времени t1= 1 с: а) перемещение x1 тележки (перемещение за время от t0= 0до t1 =l c); б) ускорение a1 тележки; в) скорость u1 тележки;г)полную нормальную реакцию N1 плоскости.
Решение. Рассмотрим механическую систему, состоящую из тележки н груза D, в произвольном положении. Изобразим действующие на систему внешние силы: силы тяжести Рь Рг и реакции плоскости N', N". Проведем координатные оси Оху так, чтобы ось у проходила через точку А0, где находился центр масс тележки в момент времени t0= 0.
a) Определение перемещения x1. Для определения x1 воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось х. Получим
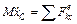 или
или 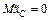 , (1)
, (1)
так как 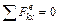 , поскольку все действующие на систему внешние силы вертикальны.
, поскольку все действующие на систему внешние силы вертикальны.
Определим значение 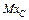 . Из рис. Д5, а видно, что в произвольный момент времени абсциссы хA – центра масс тележки и xD – груза равны соответственно:
. Из рис. Д5, а видно, что в произвольный момент времени абсциссы хA – центра масс тележки и xD – груза равны соответственно: 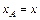 ,
, 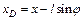 . Так как по формуле, определяющей координату хC центра масс системы.
. Так как по формуле, определяющей координату хC центра масс системы. 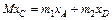 , то
, то
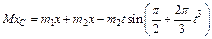 (2)
(2)
Теперь, проинтегрировав уравнение (1), найдем, что
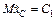 ;
; 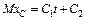 (3)
(3)
где С1 и С2 – постоянные интегрирования. Подставив во второе из этих уравнений значение МхС из равенства (2), получим
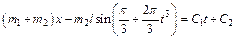 . (4)
. (4)
Для определения С1 и С2 понадобится еще одно уравнение, которое получим, продифференцировав обе части равенства (4) по времени:
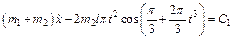 (5)
(5)
где 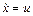 – скорость тележки. По начальным условиям при t =0, x =0,
– скорость тележки. По начальным условиям при t =0, x =0, 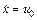 . Подставляя эти величины в равенства (4) и (5), найдем, что
. Подставляя эти величины в равенства (4) и (5), найдем, что 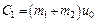 ,
, 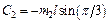 . При этих значениях C1 и С2 уравнение (4) примет вид
. При этих значениях C1 и С2 уравнение (4) примет вид
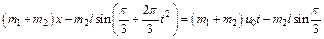
Отсюда получаем зависимость от времени координаты х, определяющей одновременно перемещение тележки;
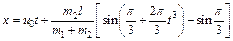 . (6)
. (6)
Полагая здесь t =1 с, найдем искомое перемещение х1. Ответ: х1= 0,33 м.
б) Определение ускорения a1. Проделав те же рассуждения и выкладки, что и в предыдущем примере, получим уравнение (1) и формулу (2). Для определения a1 продифференцируем дважды по времени обе части равенства (2). Получим
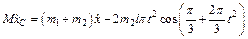 ;
;
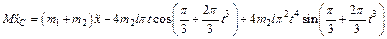 ,
,
где 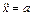 – ускорение тележки. Но согласно уравнению (1)
– ускорение тележки. Но согласно уравнению (1) 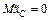 ; в результате находим следующую зависимость а от времени:
; в результате находим следующую зависимость а от времени:
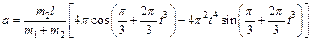 .
.
Полагая здесь t =1 с, определим искомое ускорение а1. Ответ: а1 =–2,51 м/с2. Знак минус указывает, что ускорение тележки направлено влево.
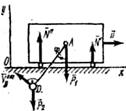
Рис Д5б
в) Определение скорости u1. Чтобы определить и1, воспользуемся теоремой об изменении количества движения системы 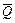 в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д5, б),то
в проекции на ось х. Так как все действующие на систему внешние силы вертикальны (рис. Д5, б),то 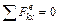 и теорема дает
и теорема дает
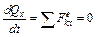 , откуда
, откуда 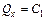 .(1)
.(1)
Для рассматриваемой механической системы 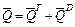 , где
, где 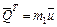 и
и 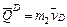 – количества движения тележки и груза D соответственно (
– количества движения тележки и груза D соответственно (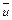 – скорость тележки,
– скорость тележки, 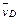 – скорость груза по отношению к осям Оху). Тогда из равенства (1) следует, что
– скорость груза по отношению к осям Оху). Тогда из равенства (1) следует, что
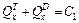 , или
, или 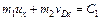 (2)
(2)
Для определения vDx рассмотрим движение груза D как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня AD вокруг оси А), а движение самой тележки – переносным. Тогда 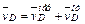 и
и
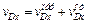 . (3)
. (3)
Но 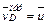 и, следовательно,
и, следовательно, 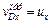 . Вектор
. Вектор 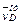 направлен перпендикулярно стержню и численно
направлен перпендикулярно стержню и численно 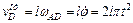 .
.
Изобразив этот вектор на рис. Д5, б с учетом знака 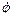 , найдем, что
, найдем, что 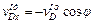 . Окончательно из равенства (3) получим
. Окончательно из равенства (3) получим
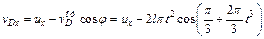 . (4)
. (4)
(В данной задаче величину vDx можно еще найти другим путем, определив абсциссу xD груза D, для которой, как видно из рис. Д5, а, получим 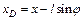 ; тогда
; тогда 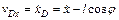 , где
, где 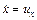 , а
, а 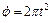 )
)
При найденном значении vDx равенство (2), если учесть, что ux=и, примет вид
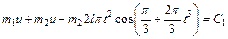 (5)
(5)
Постоянную интегрирования С1 определим по начальным условиям: при t =0 и=и0. Подстановка этих величин в уравнение (5) дает 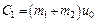 и тогда из (5) получим
и тогда из (5) получим
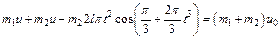
Отсюда находим следующую зависимость скорости к тележки от времени:
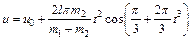 (6)
(6)
Положив в уравнении (6) t=l с, определим искомую скорость u1. Ответ: и1 =–0,76 м/с. Знак минус указывает, что скорость тележки направлена влево.
г) Определение реакции N1. Для определения N1 воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось у (см. рис Д5,а):
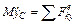 или
или 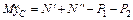 .(1)
.(1)
Отсюда, полагая 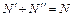 , получим
, получим
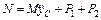 . (2)
. (2)
Из формулы, определяющей ординату yC центра масс системы, 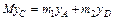 , где уA и уD – соответственно ординаты центра масс А тележки и груза D. В нашем случае
, где уA и уD – соответственно ординаты центра масс А тележки и груза D. В нашем случае 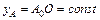 ,
, 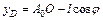 . Тогда
. Тогда
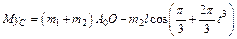 .
.
Продифференцировав обе части этого равенства два раза по времени, получим
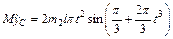 ;
;
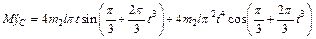 .
.
Подставив найденное выражение 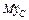 в уравнение (2), получим зависимость N от t:
в уравнение (2), получим зависимость N от t:
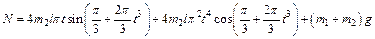 .
.
Полагая здесь t =1 с, найдем искомую реакцию N1. Ответ: N1 =68,9 Н.
 2015-10-13
2015-10-13 939
939








