2015-10-13
8446
3.1. Распределение молекул между двумя половинками сосуда.
Применим теперь элементы теории вероятности для описания одноатомного идеального газа, заключенного в сосуд объемом 
. Рассмотрим сначала распределение молекул между двумя половинками сосуда.
Введем следующую терминологию:
Макросостояние - состояние, определяемое только известным количеством частиц в каждой из половин сосуда (без уточнения их номеров и, полагая частицы неразличимыми);
Микросостояние - состояние, определяемое нахождением конкретных (по номерам) частиц в каждой из половин сосуда (известно, частицы с какими номерами находятся в левой и правой половинах сосуда).
Статистический вес (статвес) - это число равновероятных микросостояний, посредством которых реализуется данное макросостояние.
1). Если имеется всего одна молекула, то вероятность найти ее в любой половине сосуда равна
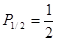(4.1).
2). Возьмем две молекулы, пронумеруем их и будем размещать их всеми возможными способами двум по половинкам сосуда. Очевидно, что всего возможны 4 (четыре) способа размещения:
 |
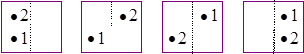Вероятность каждой из молекул оказаться в какой-либо половине сосуда равна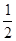 
. Поскольку положения молекул никак не зависят друг от друга, т.е. это независимые события, то, вероятность определенного размещения двух молекул сразу равна 
.
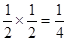3). Пусть мы теперь имеем 4 молекулы. Пронумеруем эти частицы: 1, 2, 3, 4, считая, что это возможно сделать.
Итак, каждое “номерное” размещение частиц по половинкам сосуда - это микросостояние. Понятно, что
вероятность каждого микросостояния одинакова и в случае 4-х частиц равна: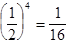 
.
Построим таблицу:
| N | Макросостояние (число частиц в половинках сосуда) левая правая | Микросостояние (частицы с разными номерами в половинках сосуда) левая правая | Статистический вес (число микросостояний, соответствующих определенному макросостоянию) | Вероятность макросостояния |
| 0 4 | - 1,2,3,4 | 1/16 | ||
| 1 3 | 1 2,3,4 2 1,3,4 3 1,2,4 4 1,2,3 | 4 ×1/16 = 1/4 | ||
| 2 2 | 1,2 3,4 1,3 2,4 1,4 2,3 2,3 1,4 2,4 1,3 3,4 1,2 | 6 ×1/16 = 3/8 | ||
| 3 1 | 1,2,3 4 1,2,4 3 1,3,4 2 2,3,4 1 | 1/4 | ||
| 4 0 | 1,2,3,4 - | 1/16 |
Полная вероятность макросостояний равна, как и следует ожидать, единице:
.
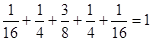Из данных таблицы видно, что наиболее вероятное макросостояние - это симметричное распределение молекул.
4). Рассмотрим, наконец, общий случай, когда в сосуде находится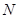 
молекул.
Будем искать вероятность реализации макросостояния, при котором находятся: слева -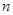 
частиц, справа - 
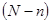частиц. Выберем одно из микросостояний: слева – частицы с номерами 
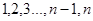; справа – с номерами 
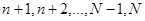. Переставляя частицы местами, учтем, что макросостояние не изменяется (число частиц остается постоянным в каждой половинке сосуда), а микросостояние изменяется, если переставляются частицы из левой половины в правую, и не изменяется, если перестановки происходят только внутри каждой половины.
Сосчитаем статвес в рассматриваемого макросостояния. Полное число возможных перестановок в системе, содержащей 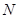частиц, равно 
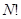. Чтобы получить число разных микросостояний в данном макросостоянии, исключим из них число перестановок внутри каждой половины, т.е., соответственно, 
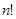и 
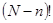перестановок. Получаем, что статистический вес выбранного макросостояния равен числу сочетаний из 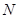по :
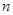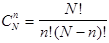(3.2)
Очевидно, что вероятность каждого микросостояния равна
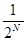(3.3)
Тогда, вероятность рассматриваемого макросостояния (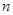 молекул слева, а 
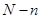молекул справа) есть
. 
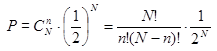(3.4)
Из полученного выражения следует, что наиболее вероятным является макросостояние, соответствующее максимальному статистическому весу, который достигается при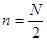 
.
Пример: Пусть в сосуде находятся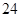 
молекулы. Вероятность того, что все молекулы соберутся в одной половине сосуда, легко вычисляется:
статвес этого макросостояния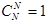 
и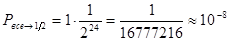 
,
т.е. вероятность такого события крайне мала уже при 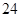молекулах.
3.2. Распределение молекул в случае произвольных объемов.
 |
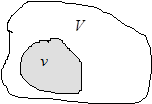Пусть в объеме находится 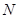молекул. Выделим в объеме меньший объем 
. Будем интересоваться макросостоянием, при котором в объеме находится 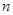частиц, а в остальной части объема 
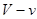содержится 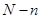молекул. Вероятность того, что в объеме находится одна молекула находится равна отношению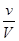 
. Вероятность, что объем содержит две частицы: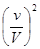 
.
Если объем содержит 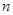частиц, то вероятность такого события - 
.
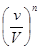В то же время остальные 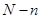молекул должны попасть в объем 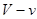, вероятность чего равна
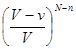
Т. о., вероятность реализации интересующего нас “микросостояния” (это условное микросостояние, т.к. клеточки пространства не одинаковы!):
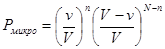(3.5)
Число способов такого распределения молекул газа в сосуде – это число соответствующих микросостояний, или статистический вес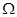 
тот же, как в случае деления сосуда на равные половинки:
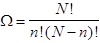
Итак, полная вероятность данного макросостояния записывается:
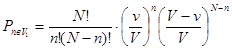(3.6)
Итак, вероятность того, что в объеме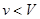 
будет обнаружено 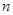частиц из 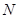, определяется формулой (3.6).
Удобно ввести обозначения: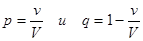 
, при этом 
.
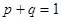Полученное распределение вероятностей называется биномиальным распределением:
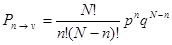. (3.7)
Биномиальное распределение (распределение Бернулли) – распределение вероятностей числа появлений некоторого события при повторных независимых испытания если вероятность появления этого события равна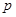 
, 
.
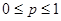Название распределения произошло от алгебраического бинома Ньютона:
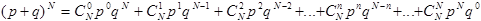. (3.8)
3.3. Свойства биномиального распределения.
1). Нормировка
Поскольку 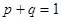, то
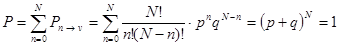, (3.9)
т.е. полная вероятность – вероятность обнаружения в малом объеме какого-либо числа частиц (от нуля до 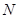включительно) – нормирована на единицу.
2). Максимум вероятности.
Сразу же возникает резонный вопрос – какое из всех возможных состояний системы (макросостояний) будет реализовываться с максимальной вероятностью? Ясно, что вероятность состояния с очень малым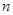и или 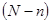при фиксированных и очень мала, т.к. при этом
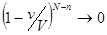или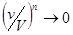 
.
Т.е. максимум вероятности должен находиться при некоторых промежуточных значениях .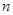
Вычисление максимума вероятности биномиального распределения.
Пусть нас интересуют достаточно большие 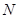и 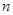, такие что переход от вероятности 
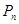к вероятности 
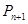осуществляется непрерывным образом и 
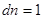- бесконечно малая величина. Чтобы найти максимум вероятности, вычислим разность вероятностей двух соседних состояний (при сделанных допущениях проведенная операция равносильна вычислению производной 
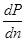) и приравняем ее нулю,:
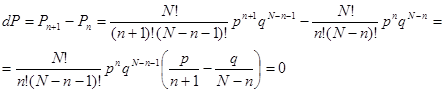(3.10)
Из равенства нулю выражения в скобках имеем
,
.
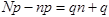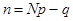Т.к.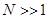 
и 
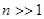, получаем что
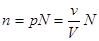. (3.11)
Вспомним, что при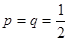 
(
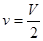, см. пункт 3.1), максимальная вероятность достигается тогда, когда максимален статвес 
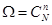, т.е. при равномерном распределении (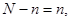
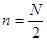) молекул газа по половинкам сосуда.
В общем случае, когда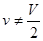 
, как показывает расчет, максимум вероятности достигается при 
.
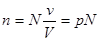Из полученного результата вытекает исключительно важное следствие. Поскольку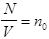 
- концентрация молекул в объеме, то наиболее вероятным является состояние системы, когда число молекул в объеме равно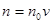 
, т.е. когда осуществляется равномерное заполнение (или распределение) молекулами всего объема сосуда.
 |
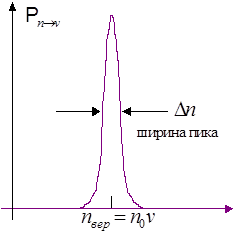Схематически картина распределения вероятности при достаточно больших значениях числах частиц 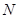и 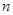выглядит как показано на рисунке (дискретные точки соединены сплошной линией): в виде острого в пика окрестности 
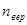c очень маленькой шириной 
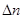. Условие нормировки может быть записано как
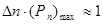(3.12)
Если за газом наблюдать достаточно большое время, то окажется, что более вероятные распределения молекул возникают чаще, чем менее вероятные. Поэтому с течением времени газ именно и переходит в наиболее вероятные состояния, причем, достигнув наиболее вероятного состояния, газ в нем практически всегда и остается.
Такое состояние называется стационарным или равновесным.
Существенно, что равновесное состояние газа не зависит от предыстории (или начального состояния), т.е. от “пути”, которым газ шел к равновесию. Независимость от предыстории и постоянство во времени свойств газа в равновесии имеют своим следствием то, что равновесный газ можно описать небольшим числом макроскопических величин, характеризующих газ в целом (для идеального газа -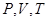 
).
Определение: равновесным состоянием системы является ее наиболее вероятное состояние.
Итак, вероятность того, что число частиц в объеме будет отклоняться даже незначительно от 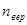ничтожна и быстро убывает с величиной этого отклонения. Но, тем не менее, число молекул в не всегда строго равно 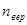, а колеблется около этой величины. Отклонения числа частиц в объеме от наиболее вероятного значения – это флуктуации.
Приложение. Вычисление максимума вероятности биномиального распределения (традиционный способ).
.
Надо решить уравнение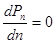 
. Будем решать это уравнение для случая, когда и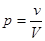 
малы, т.е. 
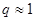, но при этом объем не слишком мал, так чтобы 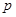не было ничтожно мало. В этом случае максимум вероятности биноминального распределения достигается при достаточно больших 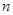и можно воспользоваться формулой Стирлинга для факториалов: 
.
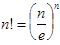Примечание. Формула Стирлинга получается следующим образом.
Возьмем логарифм от :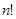
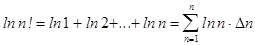, где D n = 1.
При больших 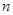можно считать 
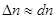. Тогда можно проинтегрировать полученное выражение
.
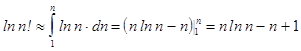Теперь потенцируем и получаем формулу Стирлинга:
.
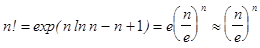Используем полученное выражение:
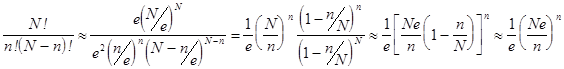
Проводя преобразования, мы воспользовались тем, что 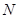велико (причем 
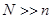) и известным пределом
.
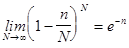Тогда имеем
.
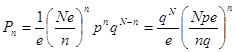Возьмем производную и приравняем её нулю 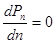, при этом вспоминая, что
.
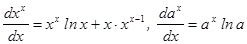Получаем
, 
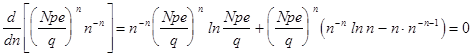
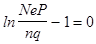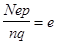
и тогда
.
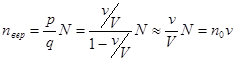Итак, развивая статистический (вероятностный) подход, мы нашли закон распределения частиц (молекул) по некоторому произвольно выбранному объему, предполагая, что в интересующем нас объеме находится газ невзаимодействующих частиц.
Среднее число частиц в произвольном объеме.
Вычислим теперь, используя распределение Бернулли, среднее число частиц в объеме по правилу, определяемому выражением (2.16)
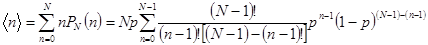, (3.13)
где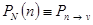 
.
Т.к. сумма, входящая в (3.13), согласно условию нормировки, равна единице, то
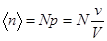. (3.14)
Заменяя в (3.6) 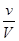на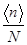 
, можем записать
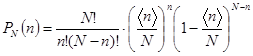. (3.15)
Сравнивая (3.11) и (3.14) сделаем ещё один важный вывод, вытекающий из статистического рассмотрения макроскопических систем. Из полученных выражений вытекает, что в состоянии равновесия наиболее вероятным числом молекул в некотором произвольно выбранном объеме является их среднее значение, что соответствует равномерному заполнению сосуда.
