Статистический метод описывает движение не отдельных молекул, а оперирует средними величинами, характеризующими движение большого числа молекул.
Идеальный газ.
Простейшей моделью обладает идеальный газ. Молекулы идеального газа не взаимодействуют (или практически не взаимодействуют) друг с другом; в равновесном состоянии движение молекул полностью хаотично. Это позволяет в грубом приближении считать, что все молекулы движутся только в направлениях X, Y и Z, т. е., если в единице объема имеется п молекул, то в каждом из этих направлений движутся по n/ З молекул, или п /6 в одну сторону.
Число ударов молекул о стенку.
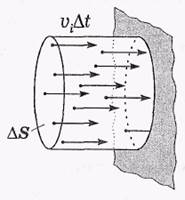
Полное число ударов молекул о единицу поверхности стенки за единицу времени определяется следующим выражением:
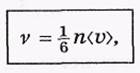
где <  > — среднее значение скорости молекул. Оценим число v для воздуха при нормальных условиях. Считая, что п ~ 1019 см"3 (порядка постоянной Лошмидта) и
> — среднее значение скорости молекул. Оценим число v для воздуха при нормальных условиях. Считая, что п ~ 1019 см"3 (порядка постоянной Лошмидта) и  ~ 1 км/с, получим
~ 1 км/с, получим
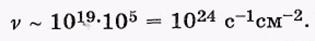
Давление газа на стенку. Природа давления - это совокупное действие множества молекул. Приращение импульса молекулы в результате столкновения
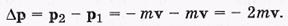
Такой же импульс, но в противоположном направлении, получила стенка.Используя закон сохранения импульса и 2-ой закон Ньютона,получим
p = 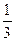 nm<
nm<  2 >.
2 >.
Это выражение можно переписать иначе:
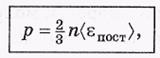
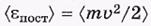 где - среднее значение поступательной кинетической энергии молекул.
где - среднее значение поступательной кинетической энергии молекул.
Эту формулу называют основным уравнением кинетической теории газов.
Физический смысл температуры Т. Сопоставив полученное выражение для давления р с уравнением Клапейрона, находим
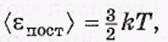
где k — постоянная Больцмана
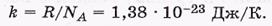
т.е.температура Т выражает среднюю кинетическую энергию молекул.
Следует обратить внимание, что <εпост> зависит только от Т, от массы же молекул не зависит. Нетрудно получить выражение
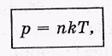
где п — концентрация молекул. Это по существу просто иная форма уравнения состояния идеального газа.
Гипотеза о равнораспределении энергии по степеням свободы
Степени свободы. Так называют число независимых координат, определяющих положение системы, или в интересующем нас случае — молекулы. Для определения положения центра масс молекулы необходимо задать три координаты. Это означает, что молекула имеет три поступательных степени свободы.
Если молекула двухатомная и жесткая(«гантель»), то, кроме трех поступательных степеней свободы, она имеет и две вращательные, связанные с углами поворота вокруг двухвзаимно перпендикулярных осей 1—1 и 2—2,
проходящих через центр масс С, как показанона рисунке
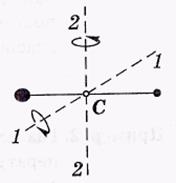
Вращение вокруг оси молекулы для материальных точек лишено смысла.
Таким образом, жесткая двухатомная молекула имеет пять степеней свободы: три поступательных и две вращательных.
Если молекула упругая, то возможны колебания атомов и необходима еще одна степень свободы (расстояние между атомами). Ее называют колебательной.
Гипотеза о равнораспределении. Средняя энергия поступательного движения молекулы равна 3/2 kT, Это означает, что на каждую степень свободы в среднем приходится энергия кТ /2. Больцман обобщил этот вывод в виде гипотезы о равном распределении средней энергии по степеням свободы. При этом на колебательную степень свободы должны приходиться в среднем по две половинки kT — одна в виде кинетической и одна в виде потенциальной (как мы знаем, их средние значения одинаковы).
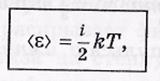 Итак, средняя энергия молекулы
Итак, средняя энергия молекулы
где i — сумма числа поступательных(z пост), вращательных (z вр) и удвоенного числа колебательных (z кол) степеней свободы:
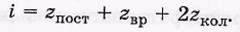
Число i совпадает с числом степеней свободы только для жестких молекул.
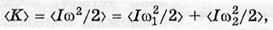 Из механики известно, что кинетическая энергия вращающегося твердого тела K=I
Из механики известно, что кинетическая энергия вращающегося твердого тела K=I 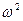 /2.В нашем случае две вращательные степени свободы, поэтому средняя вращательная кинетическая энергия
/2.В нашем случае две вращательные степени свободы, поэтому средняя вращательная кинетическая энергия
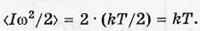 поскольку
поскольку 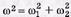 , где
, где 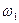 и
и 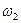 — угловые скорости вращения вокруг взаимно перпендикулярных осей, проходящих через центр масс молекулы. Ясно, что
— угловые скорости вращения вокруг взаимно перпендикулярных осей, проходящих через центр масс молекулы. Ясно, что 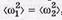 , поэтому
, поэтому
Искомая угловая скорость 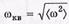 или
или

 Некоторые важные результаты для числа степеней свободы у линейных и нелинейных молекул, с учетом того, что полное число степеней свободы у системы из N материальных точек равно 3 N. приведены в таблице.
Некоторые важные результаты для числа степеней свободы у линейных и нелинейных молекул, с учетом того, что полное число степеней свободы у системы из N материальных точек равно 3 N. приведены в таблице.
Внутренняя энергия. Эта энергия для одного моля идеального газа равна
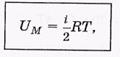
где R = kNA, а выражения для молярных теплоемкостей:

и их отношение Cp/Cv ( - постоянная адиабаты), равное
- постоянная адиабаты), равное
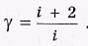
Согласно этой формуле для молекулы одноатомной  = 1,67, жесткой двухатомной
= 1,67, жесткой двухатомной  = 1,40 и упругой двухатомной
= 1,40 и упругой двухатомной  = 1,29. Эти значения хорошо согласуются с опытными данными в области комнатных температур.
= 1,29. Эти значения хорошо согласуются с опытными данными в области комнатных температур.
Расширение температурного интервала исследований показало несогласие с опытными данными.
Успех гипотезы о равнораспределении энергии по степеням свободы связан с отказом от этой гипотезы. Успех был основан на том, что некоторые степени свободы искусственно исключались без каких-либо убедительных обоснований. А если заглянуть вглубь молекулы или атома, то сразу обнаруживается, что множество степеней свободы просто проигнорировано?!
Все эти вопросы были полностью разрешены только в рамках квантовой теории, согласно которой вращательная и колебательная энергии молекулы или атома имеют дискретные значения (уровни энергии), т.е.квантованы.
Их уровни определяются соответственно формулами
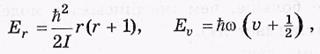
где  r — вращательное квантовое число (r = 0, 1, 2,...),
r — вращательное квантовое число (r = 0, 1, 2,...),  — колебательное (
— колебательное ( = 0, 1, 2,...), I — момент инерции молекулы относительно той или иной главной оси,
= 0, 1, 2,...), I — момент инерции молекулы относительно той или иной главной оси, 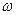 — собственная частота колебаний, h — постоянная Планка (
— собственная частота колебаний, h — постоянная Планка (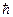 = h /2π).
= h /2π).
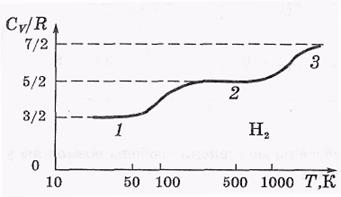
Из этих формул следует, что минимальная вращательная энергия молекулы Н2 равна порядка 0.01 эВ. И при такой низкой температуре как 50К (участок 1 на рисунке) средняя энергия поступательного движения молекулы вдвое меньше минимальной вращательной энергии.Т.е. её оказывается недостаточно, чтобы возбудить вращательные степени свободы. В этих условиях, как говорят, вращательные степени свободы «заморожены».
В области температур ~ 500К, соответствующих участку 2, вращательные степени свободы полностью разморожены, и молекула Н2 ведет себя как жесткая двухатомная молекула с числом степеней свободы 3+2 = 5. Заметим, что включаются две, а не три вращательные степени свободы. Это связано с тем, что для включения степени свободы, соответствующей вращению молекулы вокруг ее оси, проходящей через оба ядра, требуется значительно большая энергия из-за малости момента инерции молекулы относительно этой оси.
При температурах, превышающих 1000К, энергии уже оказывается достаточно для постепенного возбуждения колебательной степени свободы (полностью — нет, поскольку раньше наступает диссоциация молекулы на два атома, участок 3).
Объяснение зависимости Сv(Т), показанной на рисунке, — это серьезный успех квантовой теории.
Закон распределения по скоростям молекул газа, находящегося в термодинамическом равновесии, был найден Максвеллом (1859). (При нормальных условиях каждая молекула газа испытывает порядка 109 столкновений в секунду. С такой частотой непредсказуемо меняется модуль и направление ее скорости), но их распределение в целом остается неизменным, поскольку макросистема находится в термодинамическом (статистическом) равновесии.
Вследствие равноправности всех направлений движения расположение точек относительно начала координат будет сферически симметричным. Поэтому плотность точек может зависеть только от модуля скорости  v (но не от v).
v (но не от v).
Итак, пусть макросистема (газ) содержит N молекул. Выделим в некоторой точке — конце вектора v — малый объем dvxdydz
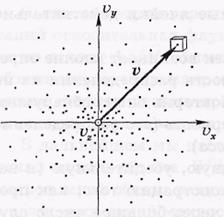
(на рисунке ось vz направлена на нас). Этот малый объем
должен быть таким, чтобы число dN молекул в нем было достаточнобольшим (во избежание заметных флуктуации). Если, например, макросистема содержит N ~ 1020 молекул, то число dN ~ 106 на много порядков меньше N, и это дает нам
право рассматривать dN как физически бесконечно малую величину,относительные флуктуации которой пренебрежимо малы. В дальнейшем под dN мы будем понимать среднее число молекул в соответствующем интервале той или иной величины.
Относительное число точек (молекул) в этом объеме dN/N, или другими словами, вероятность dP того, что скорость молекулы, т. е. конец вектора v, попадет в этот объем, можно записать так:
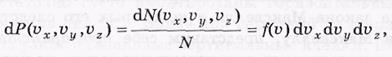
где f ( ) имеет смысл объемной плотности вероятности.
) имеет смысл объемной плотности вероятности.
Вероятность же того, что молекула (точка) будет иметь проекции скорости в интервале (vx, vx + dvx), есть
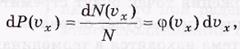
где φ (vх) — функция распределения по vx. Это выражение есть относительное число молекул (точек) в тонком плоском слое от vx до vx + dvx.
В соответствии с теоремой об умножении вероятностей независимых событий можно записать
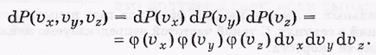
Из соображения равноправия осей vx, vy и vz следует, что функции φ должны одинаковым образом зависеть от соответствующих проекций скоростей. Поэтому
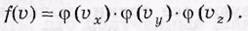
Опуская дальнейшие преобразования (с учетом условия нормировки), приведем окончательные результаты;
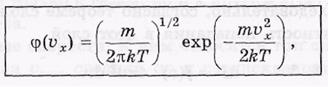
аналогичный вид имеют функции φ( у) и φ(
у) и φ( z).
z).
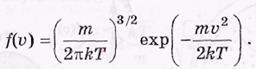 Таким образом,функция распределения по скоростям(функция Максвелла) имеет вид
Таким образом,функция распределения по скоростям(функция Максвелла) имеет вид
График функции φ (vх) изображен на рисунке
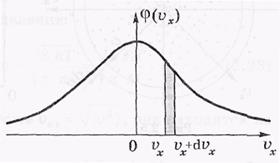
Он совпадает с гауссовой кривой погрешностей. Площадь тонированной полоски на рисунке — это вероятность того, что проекция скорости молекулы лежит в интервале, ( х,
х,  x + d
x + d  x).
x).
Функция φ ( х) нормирована на единицу, т. е. площадь под кривой φ (
х) нормирована на единицу, т. е. площадь под кривой φ ( х)
х)
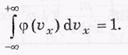
 2017-11-01
2017-11-01 1236
1236







