Тема: Комплексные числа

1. Даны два комплексных числа 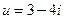и .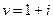

1) Запишите число 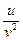в алгебраической форме.

2) Запишите число 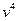в тригонометрической форме.

3) Изобразите в прямоугольной декартовой системе координат множество всех точек соответствующих комплексным числам 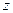, удовлетворяющим условию .

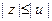4) Докажите, что для получения тригонометрической формы произведения двух комплексных чисел, заданных в тригонометрической форме, достаточно перемножить их модули а аргументы сложить.

2. Даны два комплексных числа 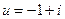и .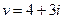

1) Запишите число 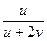в алгебраической форме.

2) Найдите все корни уравнения 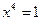и докажите, что они образуют мультипликативную группу.

3) Изобразите в прямоугольной декартовой системе координат множество всех точек соответствующих комплексным числам 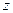, удовлетворяющим условию .

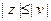4) Докажите теорему о тригонометрической форме натуральной степени комплексного числа, заданного в тригонометрической форме.