Тема: Векторные пространства

1. Даны две системы векторов арифметического векторного пространства 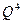над полем рациональных чисел:

(1) 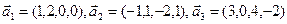и

(2) .

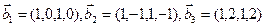1) Является ли система (1) линейно независимой?

2) Найдите базис линейной оболочки 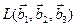системы (2).

3) Найдите размерность пространства + .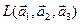

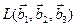4) Докажите, что совокупность все векторов пространства 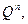у которых последняя координата равна 0, образуют подпространство векторного пространства .

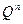2. Даны система векторов

(1) 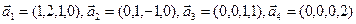и вектор 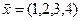арифметического векторного пространства 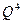над полем 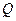рациональных чисел.

1) Образуют ли векторы системы (1) базис пространства ?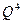

2) Определите координаты вектора 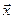в системе (1), если ответ на вопрос 1) положительный.

3) Будет ли система векторов 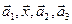линейно независимой?

4) Докажите, что если ранг матрицы координат некоторой системы векторов, заданных своими координатами в некотором базисе векторного пространства, равен числу этих векторов, то данная система векторов линейно независима.