Тема: Группы и кольца

1. Дана группа 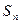подстановок n- ой степени.

1) Найдите произведение подстановок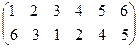

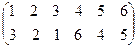
2) Вычислите порядок подстановки f = 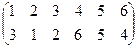в группе .

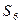3) Найдите разложение подстановки g= 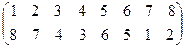в произведение независимых циклов и определите ее четность.

4) Докажите, что порядок конечной группы делится на порядок подгруппы этой группы.

2. Дано кольцо 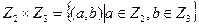с операциями определенными по правилам:

; .

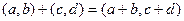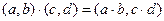1) Определите, является ли элемент 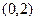делителем нуля?

2) Обратим ли элемент (1,2) в этом кольце?

3) Найдите аддитивный порядок элемента (1,1) в этом кольце.

4) Докажите, что если f: 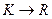– гомоморфизм колец, то подмножество 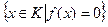является подкольцом кольца K.