1. Даны два многочлена 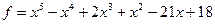 и
и 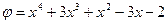 с коэффициентами из поля
с коэффициентами из поля 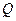 рациональных чисел.
рациональных чисел.
1) Найдите все рациональные корни многочлена 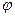 .
.
2) Найдите НОД(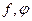 ), используя алгоритм Евклида.
), используя алгоритм Евклида.
3) Разложите многочлен 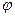 в произведение неприводимых над полем
в произведение неприводимых над полем 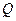 многочленов.
многочленов.
4) Докажите, что число всех корней многочлена над полем, считая кратности этих корней, не превосходит степени многочлена.
2. Даны два многочлена 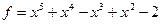 и
и 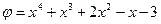 с коэффициентами из поля
с коэффициентами из поля 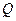 рациональных чисел.
рациональных чисел.
1) Разложите многочлен 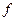 по степеням многочлена
по степеням многочлена 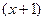 .
.
2) Найдите все рациональные корни многочлена 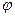 и запишите его разложение в произведение неприводимых над полем
и запишите его разложение в произведение неприводимых над полем 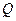 многочленов.
многочленов.
3) Найдите НОД(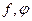 ), используя алгоритм Евклида.
), используя алгоритм Евклида.
4) Докажите, что для любого многочлена 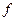 с коэффициентами из целостного кольца
с коэффициентами из целостного кольца 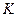 и элемента
и элемента 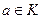 найдутся единственные многочлен
найдутся единственные многочлен 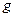 с коэффициентами из кольца
с коэффициентами из кольца 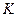 и
и 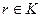 такие, что
такие, что 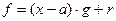 .
.
 2015-10-13
2015-10-13 655
655








