Цель: Сформировать знания о сущности, роли, значении и области применения статистического и корреляционно-регрессионного анализа

ТЕЗИСЫ ЛЕКЦИЙ

Тема 1 Статистический и регрессионный анализ

Цель: Сформировать знания о сущности, роли, значении и области применения статистического и корреляционно-регрессионного анализа.

План:

1. Прогнозирование в экономике и его информационное обеспечение.

2.Предварительный анализ данных. Теория статистического оценивания. Теория статистической проверки гипотез.

3. Доверительные области. Доверительные интервалы для зависимой переменной.

4. Теория моментов.

5. Корреляционно-регрессионный анализ.

6.Использование модели множественной линейной регрессии для прогнозирования экономических показателей.

1. Прогнозирование в экономике и его информационное обеспечение.

Прогнозирование в экономике это вид управленческой деятельности. Целью прогнозирования является описание будущего состояния экономической системы в целом или отдельных ее частей в соответствии со стоящими задачами. В строгом понимании прогноз – это научный анализ возможного будущего, построение, исследование и оценка вариантов развития экономической системы. Он предполагает внесение строгого порядка в имеющуюся информацию об экономической системе в соответствии с достаточно ясно сформулированными целями прогнозирования.

Для уяснения сущности прогнозирования необходимо сравнение с планированием. Если планирование конкретно, т.е. выполняет нормативные (предписывающие) функции, то прогнозирование – дескриптивно (описательно).

Прогноз также как и планирование может быть краткосрочным (до 3 лет), среднесрочным (5-7 лет) и долгосрочным (свыше 10 лет). Следовательно, прогноз может составляться и сопутствовать соответствующему плану. В таком случае он может оценивать вероятность выполнения плана.

Результаты такого прогнозирования служит основой для разработки перспективных планов на следующий будущий период времени.

Особенностью прогнозов на длительную перспективу является формирование возможных вариантов развития экономических систем, снабженных содержательным описанием и набором количественных показателей. Систему содержательных предпосылок, на основе которых формируются варианты прогнозов, называются сценариями.

Для разработки прогноза необходима информация. Информация может быть детерминированной и вероятностной. Причемб она может быть получена в результате планирования и прогнозирования.

Естественно, что качество информации является одним из важных факторов в разработке прогноза. Качество информации непосредственно связано с достоверностью, оперативностью получения информации и научной обоснованностью. В современных условиях это достигается за счет использования информационных и компьютерных технологий и математико-статистических методов и моделей. В свою очередь последнее возможно при наличии современной компьютерной и организационной техники, наличии вычислительных сетей и возможностей использования Интернета, технических и программных средств накопления, обработки, хранения, использования и передачи информации, телекоммуникационных связей. Большое значение имеют базы и банки данных. Понятно, что качество прогноза тем выше, чем более качественнее и больше массивы необходимой информации, чем больше возможности по оперативному поиску, получению, передаче, обработке, анализу и использованию научно-обоснованной информации.

Особое место среди факторов, повышающих качество прогнозов, занимают математико-статистические методы и модели.

2. Теория статистического оценивания. Теория статистической проверки гипотез.

Теория статистического оценивания неизвестных значений параметров или функций разрабатывает математические методы и приемы, с помощью которых на основании исходных статистических данных можно вычислить как можно более точные приближенные значения (статистические оценки) для одного или нескольких числовых параметров или функций, характеризующих функционирование исследуемой системы.

Статистическая оценка строится в виде функции от результатов наблюдений и сама является величиной случайной.

В качестве основной меры точности статистической оценки неизвестного параметра Х чаще всего используется средний квадрат ее отклонения от оцениваемого значения 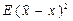, а в многомерном случае – ковариационная матрица компонент векторной оценки 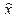(ковариационная матрица – это матрица, образованная из попарных ковариаций случайных величин). Для К-мерного случайного вектора Х=(x₁, x₂, …, x_k) ковариационная матрица – это квадратная матрица с компонентами: d_ij = E[(x_i – Ex_i) (x_j-Ex_j)]. На главной диагонали ковариационной матрицы находится дисперсии величин x_i:d_i=Dх_i. Ковариационная матрица является симметричной, т.е. d_ij = d_ji и неотрицательно определенной). Чем меньше 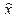, тем точнее (эффективнее) оценка. Для широкого класса генеральных совокупностей существует неравенство Рао-Крамера-Фреше, задающее тот минимум 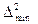(по всем возможным оценкам) среднего квадрата 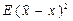, улучшить который невозможно. 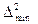используется в качестве начальной точки отсчета меры эффективности оценки, определив эффективность 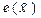любой оценки 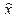параметра 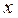в виде отношения:

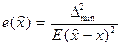(1.2.1)

Свойство состоятельности оценки 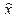обеспечивает ее статистическую устойчивость, т.е. сходимость (по вероятности) к истинному значению оцениваемого параметра 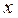по мере роста объема выборки, на основании которой эта оценка строится.

С учетом случайной природы каждого конкретного оценочного значения 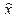неизвестного параметра 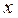представляет интерес построение целых интервалов оценочных значений 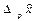, а в многомерном случае – целых областей, которые с наперед заданной (и близкой к единице) вероятностью р накрывали бы истинное значение оцениваемого параметра 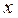, т.е. 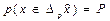. Эти интервалы (области) принято называть доверительными или интервальными оценками.

Существует два подхода к построению интервальных оценок: точный (конструктивно реализуемый лишь в сравнительно узком классе ситуаций) и асимптотически-приближенный (наиболее распространенный в практике статистических приложений).

Основными методами статистических оценок являются: метод максимального правдоподобия; метод моментов; метод наименьших квадратов; метод, использующий взвешивание наблюдений – цензурирование, урезание, порядковые статистики. Различные варианты метода, использующего и взвешивание наблюдений находят все большее распространение в связи с устойчивостью получаемых при этом статистических выводов по отношению к возможным отклонениям реального распределения исследуемой генеральной совокупности от постулируемого модельного.

Теория статистической проверки гипотез исследует процедуры сопоставления высказанной гипотезы относительно природы или величины неизвестных статистических параметров анализируемого явления с имеющимися выборочными данными.

Результат сравнения может быть отрицательным, т.е. данные наблюдения противоречат высказанной гипотезе и тогда от нее нужно отказаться либо неотрицательным, т.е. данные наблюдения не противоречат высказанной гипотезе и тогда ее можно принять в качестве допустимого решения.

По своему прикладному содержанию, высказываемые в ходе статистической обработки данных гипотезы можно подразделить на несколько основных типов:

1. Гипотезы о типе закона распределения исследуемой случайной величины. Проверка гипотез этого типа осуществляется с помощью так называемого согласия критериев и опирается на ту или иную меру различия между анализируемой эмпирической функцией распределения F(x) и гипотетическим модельным законом F_mod(x).

2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей. Например, если имеется несколько «порций» выборочных данных:

1-я: х₁₁, х₁₂, …, х_1n

2-я: х₂₁, х₂₂, …, х_2n

то говорят, что соответствующие выборочные характеристики: F_i(x) – вероятностный закон, которому подчиняются наблюдения выборки; а_i – средние значения; 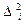- дисперсия и т.д. различаются статистически незначительно, т.е.:

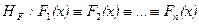(1.2.2)

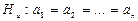(1.2.3)

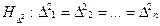(1.2.4)

3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.

Например, если а₀ – номинальное значение исследуемого параметра. Каждое отдельное значение об этом параметре х_i может отклоняться от него. Чтобы проверить исследуемое явление, например, точность настройки станка на обработку определенной детали, необходимо убедиться, что среднее значение исследуемого параметра у производимых на станке деталей будет соответствовать номиналу, т.е. проверить гипотезу:

Н: Е_у = а_i, где у – исследуемая случайная величина.

4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака.

Подобно тому как при исследовании закона распределения обрабатываемых наблюдений бывает важно правильно подобрать соответствующий модельный закон, так при исследовании статистической зависимости, например, х₂ от х₁ анализируемого двумерного признака х=(х₁, х₂) бывает важно проверить гипотезу об общем виде этой зависимости. Например, гипотезу о том, что х₂ и х₁ связаны линейной регрессионной связью, т.е.:

Н: Е(х₂ | х₁ =х) = а₀ + а₁х, (1.2.5)

где: а₀ и а₁ - некоторые неизвестные параметры модели.

Статистические критерии, с помощью которых проверяются гипотезы этого типа, часто называют критериями адекватности. По своему назначению и характеру решаемых задач они чрезвычайно разнообразны, но строятся они по одной логической схеме.

Если проверяемое предположительное утверждение сводится к гипотезе о том, что значение некоторого параметра х в точности равно заданной величине х₀, то эта гипотеза называется простой, в других случаях гипотеза называется сложной.

3.Доверительные области. Доверительные интервалы для зависимой переменной.

Доверительная область – это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. «Заданная вероятность» называется доверительной вероятностью и обычно обозначается γ. Пусть Θ – пространство параметров. Рассмотрим статистику Θ₁ = Θ₁(x₁, x₂,…, x_n) – функцию от результатов наблюдений x₁, x₂,…, x_n, значениями которой являются подмножества пространства параметров Θ. Так как результаты наблюдений – случайные величины, то Θ₁ – также случайная величина, значения которой – подмножества множества Θ, т.е. Θ₁ – случайное множество. Напомним, что множество – один из видов объектов нечисловой природы, случайные множества изучают в теории вероятностей и статистике объектов нечисловой природы.

В ряде литературных источников, к настоящему времени во многом устаревших, под случайными величинами понимают только те из них, которые в качестве значений принимают действительные числа. Согласно справочнику академика РАН Ю.В.Прохорова и проф. Ю.А.Розанова случайные величины могут принимать значения из любого множества. Так, случайные вектора, случайные функции, случайные множества, случайные ранжировки (упорядочения) – это отдельные виды случайных величин. Используется и иная терминология: термин «случайная величина» сохраняется только за числовыми функциями, определенными на пространстве элементарных событий, а в случае иных областей значений используется термин «случайный элемент». (Замечание для математиков: все рассматриваемые функции, определенные на пространстве элементарных событий, предполагаются измеримыми.)

Статистика Θ₁ называется доверительной областью, соответствующей доверительной вероятности γ, если

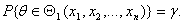(1.3.1.)

Ясно, что этому условию удовлетворяет, как правило, не одна, а много доверительных областей. Из них выбирают для практического применения какую-либо одну, исходя из дополнительных соображений, например, из соображений симметрии или минимизируя объем доверительной области, т.е. меру множества Θ₁.

При оценке одного числового параметра в качестве доверительных областей обычно применяют доверительные интервалы (в том числе лучи), а не иные типа подмножеств прямой. Более того, для многих двухпараметрических и трехпараметрических распределений (нормальных, логарифмически нормальных, Вейбулла-Гнеденко, гамма-распределений и др.) обычно используют точечные оценки и построенные на их основе доверительные границы для каждого из двух или трех параметров отдельно. Это делают для удобства пользования результатами расчетов: доверительные интервалы легче применять, чем фигуры на плоскости или тела в трехмерном пространстве.

Как следует из сказанного выше, доверительный интервал – это интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения. Границы доверительного интервала называют доверительными границами. Доверительная вероятность γ – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным. Оцениванием с помощью доверительного интервала называют способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.

Для числового параметра θ рассматривают верхнюю доверительную границу θ_В, нижнюю доверительную границу θ_Н и двусторонние доверительные границы – верхнюю θ_1В и нижнюю θ_1Н. Все четыре доверительные границы – функции от результатов наблюдений x₁, x₂,…, x_n и доверительной вероятности γ.

Верхняя доверительная граница θ_В – случайная величина θ_В = θ_В(x₁, x₂,…, x_n; γ), для которой Р(θ < θ_В) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид (-∞; θ_В].

Нижняя доверительная граница θ_Н – случайная величина θ_Н = θ_Н(x₁, x₂,…, x_n; γ), для которой Р(θ > θ_H) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид [θ_H; +∞).

Двусторонние доверительные границы - верхняя θ_1В и нижняя θ_1Н - это случайные величины θ_1В = θ_1В(x₁, x₂,…, x_n; γ) и θ_1Н = θ_1Н(x₁, x₂,…, x_n; γ) такие, что Р(θ_1H < θ < θ_1В) = γ, где θ – истинное значение оцениваемого параметра. Доверительный интервал в этом случае имеет вид [θ_1H; θ_1В].

Вероятности, связанные с доверительными границами, можно записать в виде частных случаев формулы (5):

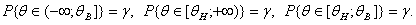(1.3.2)

В нормативно-технической и инструктивно-методической документации, научной и учебной литературе используют два типа правил определения доверительных границ – построенных на основе точного распределения и построенных на основе асимптотического распределения некоторой точечной оценки θ_n параметра θ. Рассмотрим примеры.

Пример 10. Пусть x₁, x₂,…, x_n – выборка из нормального закона N (m, σ), параметры m и σ неизвестны. Укажем доверительные границы для m.

Известно, что случайная величина

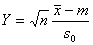(1.3.3)

имеет распределение Стьюдента с (т-1) степенью свободы, где 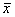- выборочное среднее арифметическое и s₀ – выборочное среднее квадратическое отклонение. Пусть 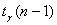и 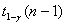- квантили указанного распределения порядка γ и 1-γ соответственно. Тогда

P { Y < t _γ(n -1)} = γ, P { Y > t _1-γ(n -1)} = γ.

Следовательно,

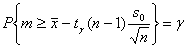(1.3.4),

т.е. в качестве нижней доверительной границы θ_Н, соответствующей доверительной вероятности γ, следует взять

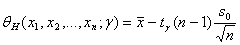. (1.3.5)

Аналогично получаем, что

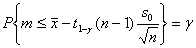(1.3.6).

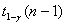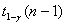
Поскольку распределение Стьюдента симметрично относительно 0, то = - 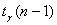. Следовательно, в качестве верхней доверительной границы θ_В для m, соответствующей доверительной вероятности γ, следует взять

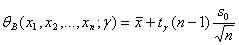. (1.3.7)

Как построить двусторонние доверительные границы? Положим

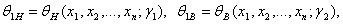
где θ_1Н и θ_1В заданы формулами (1.3.5) и (1.3.7) соответственно. Поскольку неравенство θ_1Н < m < θ_1В выполнено тогда и только тогда, когда

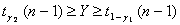(1.3.8),

то

P {θ_1H < m < θ_1B} = γ₁ + γ₂ – 1 (1.3.9),

(в предположении, что γ₁ > 0,5; γ₂ > 0,5). Следовательно, если γ = γ₁ + γ₂ – 1, то θ_1Н и θ_1В – двусторонние доверительные границы для m, соответствующие доверительной вероятности γ. Обычно полагают γ₁ = γ₂, т.е. в качестве двусторонних доверительных границ θ_1Н и θ_1В, соответствующих доверительной вероятности γ, используют односторонние доверительные границы θ_Н и θ_В, соответствующие доверительной вероятности (1+γ)/2.

Другой вид правил построения доверительных границ для параметра θ основан на асимптотической нормальности некоторой точечной оценки θ_n этого параметра. В вероятностно-статистических методах принятия решений используют, как уже отмечалось, несмещенные или асимптотически несмещенные оценки θ_n, для которых смещение либо равно 0, либо при больших объемах выборки пренебрежимо мало по сравнению со средним квадратическим отклонением оценки θ_n. Для таких оценок при всех х

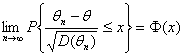(1.3.10),

где Ф(х) – функция нормального распределения N (0;1). Пусть u_γ – квантиль порядка γ распределения N (0;1). Тогда

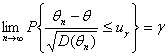(1.3.11)

Поскольку неравенство

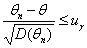(1.3.12)

равносильно неравенству

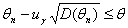(1.3.13),

то в качестве θ_Н можно было бы взять левую часть последнего неравенства. Однако точное значение дисперсии D (θ_n) обычно неизвестно. Зато часто удается доказать, что дисперсия оценки имеет вид

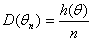(1.3.14)

(с точностью до пренебрежимо малых при росте n слагаемых), где h (θ) – некоторая функция от неизвестного параметра θ. Справедлива теорема о наследовании сходимости, согласно которой при подстановке в h (θ) оценки θ_n вместо θ соотношение (1.3.11) остается справедливым, т.е.

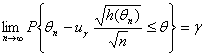(1.3.15).

Следовательно, в качестве приближенной нижней доверительной границы следует взять

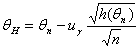(1.3.16),

а в качестве приближенной верхней доверительной границы -

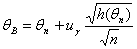(1.3.17).

С ростом объема выборки качество приближенных доверительных границ улучшается, т.к. вероятности событий {θ > θ_H} и {θ < θ_B} стремятся к γ. Для построения двусторонних доверительных границ поступают аналогично правилу, указанному выше в примере 10 для интервального оценивания параметра m нормального распределения. А именно, используют односторонние доверительные границы, соответствующие доверительной вероятности (1+γ)/2.

При обработке экономических, управленческих или технических статистических данных обычно используют значение доверительной вероятности γ = 0,95. Применяют также значения γ = 0,99 или γ = 0,90. Иногда встречаются значения γ = 0,80, γ = 0,975, γ = 0,98 и др.

4. Теория моментов.

Момент – одна из числовых характеристик распределения вероятностей

Примечание: Распределение вероятностей какой-либо действительной случайной величины Х задается в виде конечной или бесконечной последовательности ее возможных значений: х₁, х₂, х₃,…х_n,… и соответствующих им вероятностей Р (Х = х): р₁, р₂, …р_n. Вероятности должны быть положительными и в сумме давать единицу.

Например, для игральной кости это будет выглядеть в виде следующей таблицы:

Возможные значения хi
Соответствующие вероятности рi	1/6	1/6	1/6	1/6	1/6	1/6

Распределение вероятностей данного типа будет называться дискретным

Момент порядка k (k>0, целое) случайной величины Х определяется как математическое ожидание ЕХ^k случайной величины Х^k , если оно существует.

Если F(Х) – функция распределения случайной величины Х, то

ЕХ^k = 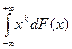(1.4.1)

при условии, что интеграл сходится абсолютно. В частности, если Х принимает значения х₁, х₂, х₃,…х_n с вероятностями р₁, р₂, …р_n, то

ЕХ^k = 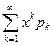. (1.4.2)

Если Х имеет плотность распределения f (х) на прямой, то

ЕХ^k = 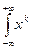, f(x) dx (1.4.3)

Примечание: плотность распределения вероятностей случайной величи6ны Х функция f(x), такая, что f(x)≥0 и 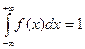, а при любых a<b вероятность события a<х<b равна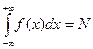

Функция распределения F(Х) случайной величины Х, если она дифференцируема связана с плотностью вероятности следующим соотношением

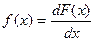. (1.4.4)

Величина Е(х-а)^k называется моментом порядка k относительно a, Е(х-Ех)^k - центральным моментом порядка k. Центральный момент второго порядка Е(х-Ех)² называется дисперсией DX.

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда. Различают: начальный момент порядка q (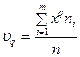) и центральный момент ().

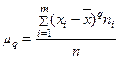С помощью центральных моментов 3 и 4 рассчитывают коэффициенты асимметрии и эксцесс.

Коэффициент асимметрии показывает скошенность (асимметрию) данных: .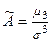

Свойства коэффициента асимметрии: 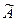>0 ряд несимметричный с правосторонней асимметрией; 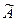<0 ряд несимметричный с правосторонней асимметрией; 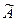=0 ряд симметричный

В то время как показывает ассиметрии характеризуют симметричность распределения растет, показатели эксцесса показывают пиковость этого распределения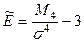

Свойства эксцесса: 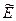>0 распределение островершинное; 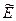<0 распределение плосковершинное; 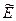=0 распределение средневершинное соответствующее нормальное.

Величина Е|х|^k называется абсолютным моментом порядка k. Аналогично определяется момент совместного распределения случайных величин х₁, х₂, х₃,…х_n(так называемого многомерного распределения): для любых целых k_i>0, k₁ + k₂+…k_n=K, математическое ожидание Е(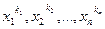) называется смешанным моментом порядка k, а Е(х₁ – Ех₁)^k1…(х_n-EX_n)^kn - центральным смешанным моментом порядка k. Смешанный момент Е(х₁-Ех₁)(х₂-Ех₂) называется ковариацией и служит одной из основанных характеристик зависимости между случайными величинами.

Если известны моменты распределения, то можно сделать некоторые утверждения о вероятностях отклонения случайной величины от ее математического ожидания в терминах неравенств. Наиболее известно неравенство Чебышева:

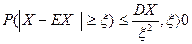(1.4.5)

и его обобщения.

Задача, состоящая в определении распределения вероятностей последовательностью его моментов, носит название проблема моментов. В математической статистике для статистической оценки параметров распределения служат выборочные моменты.

Метод моментов является одним из распространенных общих методов получения статистической оценки. Заключается в приравнивании осредненного числа выборочных моментов соответствующим моментам исходного распределения, которые являются функциями от неизвестных параметров и решения полученных уравнений относительно этих параметров.

5. Корреляционно-регрессионный анализ

Корреляционный анализ – это совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между случайными величинами или признаками (корреляция – величина, характеризующая взаимную зависимость двух случайных величин). При этом речь не идет о выявлении формы исследуемых зависимостей (это составляет предмет исследования регрессионного анализа), а лишь об установлении самого факта статистической связи и об измерении степени ее тесноты.

В качестве основных измерителей тесноты связи между количественными переменными используются: коэффициент корреляции (индекс корреляции), корреляционное отношение, парные, частные и множественные коэффициенты корреляции, коэффициенты детерминации.

Парные и частные коэффициенты корреляции являются измерителями степени тесноты линейной связи между переменными. В этом случае корреляционные характеристики могут оказаться как положительными, так и отрицательными в зависимости от одинаковой или противоположной тенденции взаимосвязанного изменения анализируемых переменных. При положительном значении коэффициента корреляции говорят о наличии положительной линейной статистической связи, при отрицательном – об отрицательной.

Коэффициент корреляции устанавливает степень зависимости между результирующим и факторным признаками (случайными величинами) и рассчитывается по формуле:

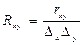(1.5.1),

где: х, у – случайные величины;

D_х, D_у – среднеквадратические (стандартные) отклонения;

r_xy – корреляционная функция или ковариация .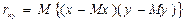

При нелинейной зависимости аналогичный показатель называется индексом корреляции.

Измерителем степени тесноты связи любой формы является корреляционное отношение, для вычисления которого необходимо разбить область значений предсказывающей переменной на интервалы группирования. Парный коэффициент корреляции позволяет измерять степень тесноты статистической связи между парой переменных без учета опосредованного или совместного влияния других показателей.

Частный коэффициент корреляции оценивает степень тесноты линейной связи между двумя переменными, очищенной от опосредованного влияния других факторов. Для его расчета необходима исходная информация как по анализируемой паре переменных, так и по всем тем переменным опосредованное, влияние которых необходимо элиминировать.

Множественный коэффициент корреляции измеряет степень тесноты статистической связи между некоторым показателем, с одной стороны, и совокупностью других переменных – с другой. Квадрат его величины (называемый коэффициентом детерминации) показывает какая доля дисперсии исследуемого результирующего показателя определяется совокупным влиянием контролируемых, объясняющих переменных. Оставшаяся необъясненной доля дисперсии результирующего показателя определяет ту верхнюю границу точности, которой можно добиться при восстановлении (прогнозировании, аппроксимации) значения результирующего показателя по заданным значениям объясняющих переменных.

В качестве основных характеристик парной статистической связи между упорядочениями используются ранговые коэффициенты корреляции Спирмэна и Кендалла. Их значения меняются в диапазоне от –1 до +1, причем экстремальные значения характеризуют связи соответственно пары прямо противоположных и пары совпадающих упорядочений, а нулевое значение рангового коэффициента корреляции получается при полном отсутствии статистической связи между анализируемыми порядковыми переменными.

В качестве основной характеристики статистической связи между несколькими порядковыми переменными используется так называемый коэффициент (согласованности) Кендалла. Между значениями этого коэффициента и значениями парных ранговых коэффициентов Спирмэна, построенных для каждой пары анализируемых переменных существуют соотношения.

Регрессионный анализ – объединяет практические методы исследования регрессионной зависимости между величинами, полученными в результате статистических наблюдений. В основе лежит понятие регрессии – зависимости среднего значения случайной величины от некоторой другой величины или нескольких величин (в последнем случае имеем множественную регрессию). Регрессионная зависимость между случайными величинами х и у характеризуется тем, что одному и тому же значению х могут соответствовать несколько значений у (например, если х – одна и та же доза минерального удобрения вносимого на 1 га почвы на разных полях, то у – урожайность разная на каждом из полей).

Уравнение, связывающее эти параметры, называется уравнением регрессии:

у = а ₀ + а ₁х + 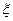(1.5.2),

где: а ₀, а ₁ - коэффициенты регрессии, которые оцениваются из статистических данных.

Аналогично записывается уравнение множественной (многофакторной) регрессии:

у = а ₀ + а ₁х₁, + … + а _nх_n+ 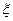(1.5.3)

Проведение регрессионного анализа условно разбивается на четыре этапа: параметризация модели; анализ мультиколинеарности и отбор наиболее информативных факторов; вычисление оценок неизвестных параметров, входящих в используемое уравнение связи; анализ эффективности полученных уравнений связи.

Таким образом, основу регрессионного анализа составляет вывод регрессионного уравнения, включающего оценку его параметров, с использованием которого находится средняя величина случайной переменной, если величина другой (других) известна. Регрессионный анализ можно считать частью теории корреляции как общей теории исследующей взаимосвязи между случайными величинами.

6.Использование модели множественной линейной регрессии для прогнозирования экономических показателей.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов экономики.

Основная цель множественной регрессии – построить модель с большим числом факторов (два и более), определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие _на моделируемый показатель.

Общий вид модели МР: у = а ₀ + а ₁х₁, + … + а _nх_n+ 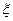(где: х₁,х₂,…х_n - факторные признаки; а ₁, а ₂,… а _n - коэффициенты регрессии при переменных х₁,х₂,…х_n, 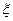- случайная ошибка). Проблема спецификации включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.

Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: они должны быть количественно измеримы; факторы не должны быть интеркоррелированы (интеркорреляция – корреляция между объясняющими переменными) и тем более находиться в точной функциональной зависимости.

Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный признак и параметры уравнения регрессии оказываются не интерпретируемыми. Если строится модель с набором p факторов, то для нее рассчитывается показатель детерминации 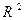, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии факторов. Влияние других не учтенных в модели факторов оценивается как 1- 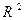с соответствующей остаточной дисперсией ().

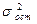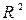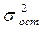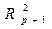
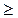
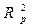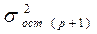
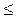
При дополнительном включении в регрессию p +1 фактора должен возрастать, а уменьшаться: и 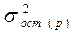. Если этого не происходит, то включаемый в анализ фактор 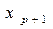не улучшает модель и является лишним фактором.

Отбор факторов осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции.

Как и в парной регрессии различают линейные и нелинейные уравнения множественной регрессии (МР).

В линейной МР 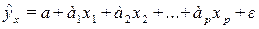параметры при х (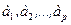) называются коэффициентами «чистой» регрессии, которые характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленных на среднем уровне. Параметр а не подлежит экономической интерпретации.

Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбирать ту, для которой 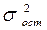и ошибка аппроксимации минимальны, а коэффициент детерминации (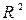) максимален.

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации.

Показатель множественной корреляции оценивает тесноту совместного влияния факторов на результат.

Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера: 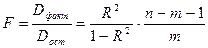(где: 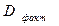- факторная сумма квадратов отклонений на одну степень свободы; 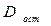- остаточная сумма квадратов на одну степень свободы; 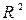- коэффициент (индекс) множественной детерминации; 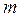- число параметров при переменных х; 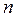- число наблюдений.

Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если 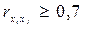(r_x1x2 – коэффициент корреляции, отражающий межфакторную связь между признаками х₁ и х₂). Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: затрудняется интерпретация параметров множественной регрессии; оценки параметров не надежны.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии: метод исключения; метод включения; шаговый регрессионный анализ. Каждый из этих методов по-своему решает проблему отбора факторов и дает, в целом, близкие результаты – отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ или метод включения-исключения). В целом, данные методы называют методами пошаговой регрессии.

Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится регрессия.

Литература: О.:11 (гл.5,с.281-297); 9 (гл. 17.4 с.326-329).

Д.: 6 (с.146-152)18 (гл.4 с.52-92); 17 (гл.6 с.157-187); 9 (гл.5 с.189-231, с.276-282)

Контрольные вопросы:

1. Назовите цель прогнозирования экономической системы.

2. Программное обеспечение статистического анализа.

3. Какие виды статистических оценок вы можете перечислить?

4. Какие требования предъявляются к статистическим оценкам параметров распределения?

5. Дайте определение ковариации и опишите метод моментов.

6. Дайте определение ассиметрии и эксцесса, укажите формулы расчета данных показателей.

7. Дайте определение множественной регрессии, анализ ее коэффициентов.

8. Дайте определение парной регрессии, анализ ее коэффициентов.

9. Особенности применения линейной и нелинейной регрессии.

10. Дайте определение коэффициента корреляции, укажите формулу расчета данного показателя.

11. Назовите разницу между линейной и функциональной связью.

12. Назовите и отразите модели нелинейной регрессии.