Моделирование сезонных и циклических колебаний

Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания. Простейший подход – расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели: 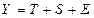. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (Т), сезонной (S) и случайной (E) компонент.

Общий вид мультипликативной модели: 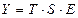. Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (Т), сезонной (S) и случайной (E) компонент.

Построение аддитивной и мультипликативной моделей сводятся к расчету значений Т, S и E для каждого уровня ряда.

До работы с временными рядами необходимо произвести предварительный анализ. Он заключается в выявлении и устранении аномальных значений уровня ряда, а также в определении наличия тренда. Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и которое оказывает существенное влияние на значение основных характеристик ряда, в том числе на соответствующую трендовую модель. При наличии аномальных наблюдений могут быть ошибки технического порядка или ошибки первого или второго рода. Ошибки первого рода возникают при агрегировании и дезагрегировании показателей, при передаче информации и по другим причинам. Они подлежат выявлению и устранению.

К ошибкам второго рода относятся аномальные уровни, которые могут возникнуть из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически, редко. Эти ошибки устранению не подлежат.

Для выявления аномальных уровней временных рядов используются следующие методы, рассчитанные для статистических совокупностей: метод Ирвина, метод проверки разностей средних уровней, метод Фостера-Стьюарта.

Как правило, уровни рядов динамики колеблются и, как следствие, тенденция изменения ряда получается скрытой. С целью выявления тенденции изменения экономического ряда динамики для применения методов прогнозирования с помощью трендовых моделей, необходимо провести сглаживание (выравнивание) врменного ряда.

Методы сглаживания экономических рядов динамики делятся на следующие две группы:

1.Аналитическое выравнивание с использованием кривой проведенной между конкретными уровнями ряда, определяющую основную тенденцию изменения ряда и освобождающую его от незначительных колебаний.

2.Механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней.

Одним из методов моделирования временного ряда, содержащего сезонные колебания, является построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний.

Пусть имеется временной ряд, содержащий циклические колебания периодичностью k. Модель регрессии с фиктивными переменными для этого ряда будет иметь вид:

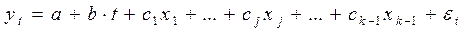где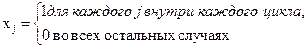

Основной недостаток модели с фиктивными переменными для описания сезонных и циклических колебаний – наличие большого количества переменных.

4. Сглаживание временных рядов.

Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций: линейный тренд; гипербола; экспоненциальный тренд; тренд в форме степенной функции; парабола второго и более порядков.

Параметры каждого из перечисленных выше трендов можно определить обычным методом наименьших квадратов, используя в качестве независимой переменной время 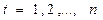, а в качестве зависимой переменной – фактические уровни временного ряда 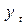. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных относятся: качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровн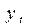и и 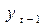тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Методы выравнивания основаны на использовании различных выравниваний функций, параметры которых обычно находят методом наименьших квадратов. Уровни выравнивания ряда выражаются в виде функции:

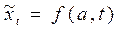(2.4.1),

где: 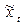- уровень выровненного ряда;

f – выравнивающая функция;

а – вектор параметров;

t – время.

Из выравнивающих функций наиболее часто используются: линейная (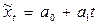) - ей соответствует постоянство абсолютных приростов временного ряда); полином заданной степени 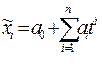- ему соответствует постоянство n-ых последовательных разностей временного ряда); логистическая функция или кривая Перла-Рида – возрастающая функция (наиболее часто выражается в виде 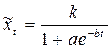, где: a,b – положительные параметры, k – предельное значение функции при бесконечном возрастании времени. Экспоненциальная функция ( 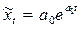- ей соответствует постоянство удельного прироста временного ряда). Среди методов сглаживания наиболее часто применяются следующие. Простая скользящая средняя по 2 l +1 членам задается формулой:

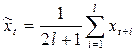(2.4.2),

где x_t – уровень исходного ряда, l ³ 1.

Сглаживание центрированной средней осуществляется с использованием формулы:

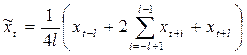(2.4.3),

которая получается попарным усреднением соседних результатов простой скользящей средней по 2 l членам.

Повторное попарное усреднение состоит в вычислении взвешенной скользящей средней с весами, пропорциональными коэффициентам биномиального ряда:

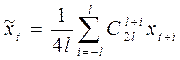(2.4.4)

Сглаживание скользящим полиномом состоит в локальной полиномиальной аппроксимации уровней исходного ряда, т.е. в сглаживании центрального из каждых 2l+1 соседних уровней ряда полинома заданной степени, доставляющим минимум суммы квадратов отклонений от уровней исходного ряда. Этот метод сводится к взвешенной скользящей средней, отдельные веса которой отрицательны.

5.Динамические модели с распределенными лагами.

Для оценки лаговой структуры зависимости было разработано несколько подходов, позволяющих ограничить число объясняющих переменных в уравнении регрессии с целью избежать появления проблемы мультиколлинеарности или минимизировать её эффект.

Рассмотрим два широко известных подхода: метод Койка и «Алмон».

В распределении Койка делается простое предположение, что коэффициенты («веса») при лаговых значениях объясняющей переменной убывают в геометрической прогрессии. Если имеется единственная объясняющая переменная, то модель принимает вид:

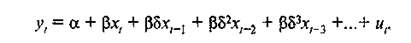(2.5.1)

где значение δ находится в границах от —1 до 1. Во многих приложениях предполагается, что оно лежит между 0 и 1. В данной зависимости имеются всего три параметра: а, β и δ.

Рассмотрим все значения 0,00, 0,01, 0,02 и т. д., увеличивая их каждый раз на 0,01. Чем меньше шаг, тем более точными будут полученные результаты, но тем больше времени займут расчеты. Теперь, когда компьютеры стали такими мощными и дешевыми, можно достичь любой желаемой точности. Для каждого значения δ рассчитывается:

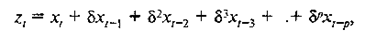(2.5.2)

с таким значением p, при котором дальнейшие лаговые значения х не оказывают существенного воздействия на z Затем оценивается уравнение регрессии:

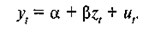(2.5.3)

Эти расчеты проводятся для всех значений δ и выбирается такое значение δ, которое обеспечивает наибольший коэффициент R² при оценке уравнения. В качестве оценок а и β выбираются их оценки в этом уравнении.

Метод «Алмон» использует так называемое преобразование Койка. Если выражение выполняется для периода t, то оно также выполняется для периода t-1:

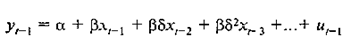(2.5.4)

Умножив обе части этого уравнения на δ и, вычтя их из уравнения (2.5.1) получим:

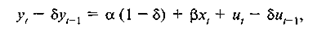(2.5.5)

где уже отсутствуют лаговые значения х. Как следствие имеем:

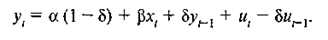(2.5.6)

Эта форма позволяет анализировать кратко- и долгосрочные динамические свойства модели. В краткосрочном аспекте (в текущем периоде) значение y_t_-1нужно рассматривать как фиксированное, и воздействие x на y отражается коэффициентом β. В долгосрочном периоде (не учитывая случайный член), если x_t, стремится к некоторому своему равновесному значению 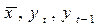также будут стремиться к равновесному уровню 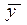,определяемому как

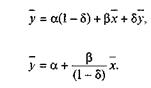
из которого следует:

(2.5.7)

Распределение Койка основывается на ограничивающем предположении, что коэффициенты при лаговых объясняющих переменных убывают в геометрической прогрессии. Для многих исследований это предположение вполне удовлетворительно, но для других оно малореалистично. Например, в некоторых случаях более уместно предположить, что изменение зависимой переменной в ответ на изменение объясняющей переменной сначала невелико, затем возрастает со временем, а потом снова уменьшается. Распределенные лаги «Алмон» (Almon, 1965) обладают достаточной гибкостью для моделирования поведения такого рода, используя при этом минимальное число параметров.

В основе модели лежит предположение о том, что если у зависит от текущих и лаговых значений х, то веса в этой зависимости подчиняются полиномиальному распределению. По этой причине лаги «Алмон» также часто описываются как полиномиально распределенные лаги. Приведем простые примеры, когда значения весов подчиняются квадратичной зависимости кубической функции или полиному более высокой степени. Выбор функции остается за исследователем, и он, конечно, может быть сделан на основе экспериментов

В общем случае модель регрессии может быть записана как

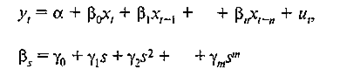(2.5.8)

Далее исследователь должен выбрать число лаговых значений п объясняющей переменной,которое будет использоваться в модели. И снова это число может быть определено в результате экспериментов, направленных на получение хорошего описания, имеющихся данных.

На практике распределение лагов объясняющей переменной может не соответствовать простой функции, и попытки их применения могут привести к нежелательным результатам: получение весов с неверными знаками, резкое уменьшение весов на краю распределения и т. д. Все эти проблемы в принципе можно преодолеть, используя полиномы более высокой степени: сама Ш. Алмон в своей статье использовала полином четвертой степени, получив вполне удовлетворительные результаты. Однако с ростом степени полиномов вновь возникает риск появления неучтенной мультиколлинеарности. Число переменных z равно числу слагаемых в полиноме, и переменные z коррелируют друг с другом, поскольку каждая из них является линейной комбинацией текущего и лаговых значений х.

6. Стационарные временные ряды.

Набор случайных переменных 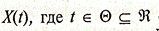(вещественные числа) называется стохастическим процессом. Дискретный стохастический процесс определяется как последовательность случайных переменных 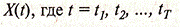или короче Х₁, Х₂,...,Х_т..., или просто Х_t.

Математическое ожидание Е(Х_t) может изменяться во времени и представляет собой функцию среднего в зависимости от времени

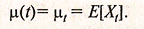(2.6.1)

Аналогичным образом дисперсия (Х_t) является функцией, также зависящей от времени:

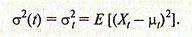(2.6.2)

В общем случае в каждый момент времени существует определенная дисперсия. Это не то же самое, что изменчивость эмпирических данных по мере развития процесса во времени.

Конечная реализация х₁, х₂,..., Х_Т дискретного стохастического процесса... Х₁, Х₂,... Х_Т... называется временным рядом.

Процессы обозначаются прописными буквами, обозначают временные ряды сточными буквами. Исключениями являются остатки в моделях стохастических процессов, не имеющие никакой самостоятельной практической значимости. Они также обозначаются строчными буквами, например а, и или ε. Строгое разграничение необходимо для корректного вывода свойств временных рядов из свойств стохастических процессов. Позднее при моделировании реальных временных рядов это условие можно будет ослабить или опустить.

Стохастический процесс Х_t, называется стационарным в сильном смысле, если совместное распределение вероятностей всех переменных Х_t₁, Х_t₂,..., Х_tn точно то же самое, что и для переменных Х_t₁₊_r, Х_t₂₊_r,..., Х_tn₊_r

Под стационарным процессом в слабом смысле понимается стохастический процесс, для которого среднее и дисперсия независимо от рассматриваемого периода времени имеют постоянное значение, а автоковариация зависит только от длины лага между рассматриваемыми переменными.

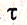
Автоковариация как функция длины лага

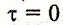
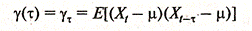(2.6.3)

называется автоковариационной функцией. При ее значение равно дисперсии.

Проведя нормировку 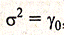, получим автокорреляционную функцию стационарного стохастического процесса:

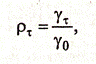(2.6.4)

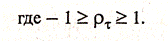
Временной ряд Х₁, Х₂,..., Х_Т, т. е конкретная реализация стационарного стохастического процесса Х_t, также называется стационарным.

В практической аналитической работе стационарность временного ряда означает отсутствие:

- тренда,

• систематических изменений дисперсии,

• строго периодичных флуктуаций,

•систематически изменяющихся взаимозависимостей между элементами временного ряда.

Экономические временные ряды представляют собой данные наблюдений за экономическими показателями, например, валовым внутренним продуктом за ряд лет, и такие ряды, как правило, не стационарны.

Основная проблема в оценивании параметров распределения процесса состоит в том, то в общем случае размер выборки n=1, поскольку обычно имеется единственная реализация процесса. Ввиду этого сделать осмысленную оценку практически невозможно. Изучаемый стохастический процесс как таковой неизвестен. Его стационарность или нестационарность может быть установлена только посредством анализа соответствующего ему временного ряда. Но, с другой стороны, многие методы анализа временных рядов предполагают их стационарность. Это приводит к своего рода замкнутому кругу, когда свойство, на наличие которого проводится исследование входит в изначальные предпосылки.

Данную проблему можно решить с использованием понятия эргодичность: это поведение большого класса стационарных процессов, когда арифметическое среднее со временем сходится к математическому ожиданию μ. Эргодичность делает возможным оценивание μ (математическое ожидание), σ²(дисперсия), γ(τ) (автоковариация) стохастического процесса только по его реализации — временному ряду.

Известны различные подходы к распознаванию стационарности временных рядов:

- графическое представление временного ряда и визуальная проверка на наличие какого-либо тренда, т.е. меняющегося среднего, увеличивающейся или уменьшающейся дисперсии устойчивых периодичностей;

- исследование на наличие автокорреляции в реальных данных;

- тесты на присутствие детерминистического тренда, например t-тест на коэффициенты оценок метода наименьших квадратов;

- тесты на наличие стохастического тренда, например тесты на единичный корень.

Процесс называется нормальным, если совместное распределение Х_t₁, Х_t₂,..., Х_tn — это n-мерное нормальное распределение. В данном случае из стационарности в слабом смысле следует стационарность в сильном смысле.

«Белым шумом» называется число случайных процессов, т.е. ряд независимых, одинаково распределенных случайных величин. Главные свойства «белого шума» следующие:

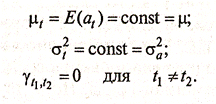(2.6.5)

Из этого очевидным образом следует стационарность. «Белый шум» играет важную роль при моделировании остатков или шоков стохастического процесса, генерирующего данные (временной ряд).

7. Тестирование стационарности

Идентификация рядов, основанная на проверке постоянства среднего, дисперсии и ковариации невозможна, так как априори структура ряда неизвестна. Для получения критерия, который можно было бы использовать для выявления нестационарности рядов, рассмотрим авторегрессионный процесс У_t первого порядка:

(2.7.1)

Не сложно проверить, что при |α₁| < 1 условия стационарности выполняются, а при α₁= 1 — не выполняются, Т.е. в первом случае говорят о стационарном, а во втором случае — о нестационарном процессе у_t, поэтому нестационарные процессы называются также процессами единичного корня.

Между стационарными и нестационарными временными рядами имеется существенное отличие. Единовременное шоковое воздействие на стационарный ряд носит временный характер. Со временем эффект рассеивается и значения временного ряда возвращаются к своему долгосрочному среднему значению. Следовательно, долгосрочный прогноз стационарного ряда сходится к безусловному среднему. Для облегчения идентификации стационарных рядов будем использовать следующие свойства:

1. Уровниряда колеблются вокруг постоянного долгосрочного среднего значения.
2. Временной ряд имеет постоянную, не зависящую от времени дисперсию.
З. Временной ряд имеет теоретическую коррелограмму, которая убывает при возрастании длины лага.

С другой стороны, ряды обязательно имеют постоянную компоненту, среднее и/или дисперсия не постоянны, т.к. зависят от времени. Перечисленные ниже свойства помогут идентифицировать нестационарные временные ряды.

1. В долгосрочном периоде не существует постоянного среднего значения, к которому возвращаются значения временного ряда.

2. Дисперсия зависит от времени и по мере увеличения времени растет до бесконечности.
3. Теоретическая автокорреляция не сокращается, но для наблюдений, ограниченных некоторыми пределами медленно затухает.

Для формального определения стационарности ряда эти свойства не подходят. В основу тестов на идентификацию временных рядов положена проверка условия равенства или неравенства параметра α₁единице из уравнения

. (2.7.2)

Это так называемые тесты единичного корня.

С одной стороны, большинство экономических временных рядов нестационарны, а с другой стороны, многие методы и модели основаны на предположении о стационарности временных рядов.

Во многих случаях взятие разностей временных рядов позволяет получить стационарные временные ряды.

Первые разности стохастического процесса имеют вид:

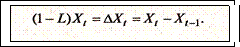(2.7.3)

Или для сезонного процесса с длиной периода s:

(2.7.4)

Если первые разности ряда Х_t стационарны, то ряд Х_t называется интегрируемым первого порядка.

В противном случае дальнейшее взятие разностей приведет ко вторым разностям:

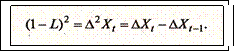(2.7.5)

Если этот ряд стационарен, то ряд Х_t называется интегрируемым второго порядка. Если мы получаем первый стационарный ряд после k-кратного взятия разностей, процесс называется интегрируемым k-го порядка. Временной ряд, сгенерированный случайным процессом, интегрируемым k-го порядка, также называется интегрируемым k-го порядка.

Пример. Пусть X_t= a_t — «белый шум». Очевидно, что он по крайней мере слабо стационарен, так как Е(а_t) (математическое ожидание) = μ и vаr (а_t) (вариация)=σ_a²(дисперсия)постоянны. Поскольку элементы а_t, а_t_-1,... процесса по определению независимы, ковариация

(2.7.6)

будет постоянно равна нулю, т.е. не будет зависеть от времени.

Пример. Процесс X_t = X_t_-1+a_t (2.7.7)

где а_t— «6елый шум» называют случайным блужданием. Он нестационарен, его характеристическая функция имеет единичный корень: z=1. Среднее x_t Е(х_t) = Е(х_t_-1)+ Е(а_t)=μ постоянно.

Нестационарность может быть доказана только посредством изучения дисперсии.

Это означает зависимость var (Х_t) от времени t. Ряд Х_t в таком случае называют процессом с нестационарной дисперсией. Первые разности Х_t являются «белым шумом» а_t и стационарны Δx_t = x_t – x_t_-1 = a_t.

Следовательно, случайное блуждание — интегрируемый процесс первого порядка. Известно, что кажущийся очень похожим процесс У_t= 0,999У_t_-1 + а_t, при z=1,001 лежит вне единичного круга, является стационарным. Таким образом, одна из наиболее серьезных проблем в анализе временных рядов состоит в том, чтобы корректно провести различие между временными рядами х_t и у_t как случайными реализациями соответственно процесса единичного корня Х_t и стационарного процесса Y_t. Для решения этой задачи полезны тесты на единичный корень.

Наиболее простой способ проверки на стационарность временного ряда — применение интеграционной статистики Дарбина-Уотсона (IDW - статистика) для авторегрессии первого порядка вида

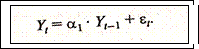(2.7.8)

Разработанная на основе статистики Дарбина—Уотсона для анализа автокорреляции остатков IDW-статистика имеет следующий вид:

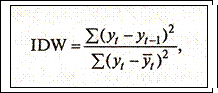(2.7.9)

Если временной ряду y_t— нестационарный, т.е. в уравнении (2.7.8) α₁=1, тогда имеем выражение в числителе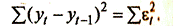

Ясно, что для нестационарного ряда это отношение будет близко к 0. Можно сказать, что процесс у_t— не стационарный, если значение IDW≈0, и достаточно уверенно утверждать, что у_t — стационарный, если значение IDW≈2.

Утверждение о стационарности процесса не требует подтверждения результатами других тестов, однако нестационарность ставит задачу определения порядка интегрируемости, либо заключения о том, что процесс неинтегрируем вообще.

Как правило, исследователю не известно заранее, какие компоненты содержит временной ряд, включает ли он свободный член или тренд. Поэтому использование интеграционной статистики Дарбина—Уотсона на этапе оценки интегрируемости временных рядов без применения дополнительных тестов может привести к ошибочным выводам и повлечь за собой неправильную спецификацию регрессионных уравнений.

Для оценки стационарности или порядка интегрируемости рассматриваемых временных рядов необходимо сопоставить расчетные значения IDW-статистики с критическими. Поскольку распределение IDW -статистики не соответствует ни одному из известных теоретических распределений, критические значения будут представлены не единичными значениями, а интервалами прямой в окрестности точки 2. Для выявления нестационарных временных рядов таблица критических значений составляется из отрезков прямой в окрестности точки 0.

Критические значения из таблицы «Критические значения интеграционной статистики Дарбина-Уотсона (см. И.И.Елисеева, С.В.Курышева, Т.В.Костеева. Эконометрика:Учебник/Под ред. И.И.Елисеевой.-2-е изд., перераб. и доп..- М: Финансы и статистика, 2005г.-576с.) для оценки стационарных временных рядов» применяются для проверки гипотезы Н₀:IDW=2 (рассматриваемый процесс стационарный) и альтернативной ей гипотезы Н₁:IDW≠2 (рассматриваемый процесс не является стационарным). Для проверки гипотезы Н₀:IDW=0 (процесс нестационарный) и альтернативной гипотезы Н₁:IDW≠0 (процесс не является не стационарным) используется таблица «Критические значения интеграционной статистики Дарбина-Уотсона для оценки нестационарных временных рядов». Механизм проверки гипотезы о стационарности и нестационарности временного ряда представлен на рисунке 2.7.1

Тестируемый временной ряд нестационарен. Нет оснований отклонить гипотезу Но				Тестируемый временной ряд стационарен№ Нет оснований отклонить гипотезу Но



0 IDW^//	IDWu^//	IDW_L^//	IDWu^/

Рис 2.7.1. Механизм проверки гипотезы о стационарности временного ряда.

Таким образом, для применения интеграционного критерия Дарбина-Уотсона расчетное значение IDW-статистики необходимо сравнить с нижним критическим значением из таблицы «Критические значения интеграционной статистики Дарбина-Уотсона для оценки нестационарных временных рядов», и если выполняется соотношение IDW_расч<IDW^II_L, тогда на соответствующем уровне значимости гипотеза о нестационарности временного ряда не может быть отклонена. Если между расчетным и верхним критическим значением из таблицы «Критические значения интеграционной статистики Дарбина-Уотсона для оценки нестационарных временных рядов» выполняется соотношение IDW_расч>IDW^I _U, тогда на соответствующем уровне значимости нет оснований отклонить гипотезу о стационарности временного ряда.

8. Коинтеграция временных рядов.

Общий недостаток методов исключения тенденции заключается в том, что эти методы предполагают некоторую модификацию модели вследствие либо замены переменных, либо добавления в эту модель фактора времени, Однако большая часть соотношений, постулируемых экономической теорией, верификацией которых занимается эконометрика, сформулирована в терминах уровней временных рядов, а не их последовательных разностей или отклонений от трендов и предполагает измерение взаимосвязи переменных без включения в модель каких-либо дополнительных факторов (например, переменной времени).

В ряде случаев наличие в одном из временных рядов тенденции может быть следствием именно от того факта, что другой ряд, включенный в модель, тоже содержит тенденцию, а не просто является результатом прочих случайных причин. Поэтому одинаковая или противоположная направленность тенденций рядов может иметь устойчивый характер и наблюдаться на протяжении длительного промежутка времени, а коэффициент корреляции, рассчитанный по уровням временных рядов, может соответственно не содержать ложной корреляции и характеризовать истинную причинно-следственную связь между ними.
Начиная с 1970-х гг. эти предположения были положены в основу новой теории о коинтеграции временных рядов. Под коинтеграцией понимается причинно-следственная зависимость в уровнях двух (или более) временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.

Не останавливаясь детально на положениях и концепциях теории коинтеграции (глубокое ее рассмотрение потребовало бы подготовки отдельного учебного пособия), в данном разделе мы кратко охарактеризуем основные статистические методы и критерии, применяемые для проверки гипотез о наличии коинтеграции временных рядов данных.
В соответствии с этой теорией между двумя временными рядами коинтеграция существует в случае, если линейная комбинация временных рядов — это стационарный временной ряд (т. е. ряд, содержащий только случайную компоненту и имеющий постоянную дисперсию на длительном промежутке времени).

Рассмотрим уравнение регрессии вида y_t=a+bx_t+ε_t. Остатки ε_t в этом уравнении представляют собой линейную комбинацию рядов у_t, и х_t: ε_t= y_t – a – bx_t (2.8.1)

Если результаты тестирования показывают, что фактическое значение критерия Дарбина - Уотсона нельзя признать равным нулю (т. е. оно превышает критическое значение для заданного уровня значимости), нулевую гипотезу об отсутствии коинтеграции временных рядов отклоняют.

Если фактическое значение критерия Дарбина — Уотсона меньше критического значения для заданного уровня значимости, то нулевая гипотеза об отсутствии коинтеграции не отклоняется.

Коинтеграция двух временных рядов значительно упрощает процедуры и методы, используемые в целях их анализа, поскольку в этом случае можно строить уравнение регрессии и определять показатели корреляции, применяя в качестве исходных данных непосредственно уровни изучаемых рядов, учитывая тем самым информацию, содержащуюся в исходных данных, в полном объеме. Однако поскольку коинтеграция означает совпадение динамики временных рядов в течение длительного промежутка времени, то сама эта концепция применима только к временным рядам, охватывающим сравнительно длительные (например, в несколько десятилетий) промежутки времени. При наличии коротких временных рядов данных, даже если формальные критерии показали присутствие их коинтеграции, моделирование взаимосвязей по уровням этих рядов может привести к неверным результатам ввиду нарушения предпосылок теории коинтеграции.

Литература: О.: 14 (гл.5 с. 154-160).

Д.: 9 (гл.4 с.144-189, гл.5 с.189-231), 17 (гл.6 с. 157-187)

Контрольные вопросы:

1. Дайте определение временного ряда.

2. Перечислите компоненты временного ряда.

3. Опишите динамические модели с распределенными лагами.

4. Опишите стационарные временные ряды.

5. Опишите нестационарные временные ряды.

6. Дайте определение термину «белый шум».

7. Назовите методы тестирования стационарности временного ряда.

8. Дайте определение процесса коинтеграции временных рядов.

9. Особенности применения интеграционной статистики Дарбина-Уотсона.