Цель: Сформировать знания о сущности, роли, значении и области применения прогнозирования временных рядов

План:

1. Адаптивные и мультипликативные методы прогнозирования.

2. Экспоненциальное сглаживание.

3. Авторегрессионные модели.

4. Модели скользящего среднего.

5. Интегрированные процессы. Идентификация авторегрессионной модели скользящего среднего.

6. Доверительные интервалы прогноза.

7. Предсказание доходности и волатильности на финансовых рынках.

8. Прогнозирование социально-экономических процессов.

1. Адаптивные и мультипликативные методы прогнозирования. Прогнозирование с моделями временных рядов.

Адаптивные модели прогнозирования позволяют дисконтировать (приводить к сопоставимому виду) данные и способные быстро адаптировать свою структуру и параметры к изменению условий.

При оценке параметров адаптивных моделей, в отличие от рассмотренных выше, наблюдениям (уровням ряда) присваиваются различные веса в зависимости от степени их влияния на текущий уровень. Это позволяет учитывать любые колебания, в которых прослеживается закономерность. Все адаптивные модели основываются на двух схемах: скользящего среднего (СС-модели) и авторегрессии (АР-модели).

В СС-модели оценкой текущего уровня является взвешенное среднее всех предшествующих уровней. По мере удаления от последнего уровня веса при наблюдениях убывают, т.е. информационная ценность наблюдений тем выше, чем она ближе к концу интервала, выделенного для наблюдений.

______________________________________________________________________________________

* Статистические критерии, предназначенные для проверки гипотезы о коинтеграции, основаны не на проверке стационарности остатков, а на проверке менее жесткой гипотезы — гипотезы об отсутствии во временном ряде единичного корня

В АР-модели оценкой текущего уровня является взвешенная сумма не всех, а нескольких предшествующих уровней. Весовые коэффициенты не ранжируются. Информационная ценность наблюдений определяется не их близостью к моделируемому уровню, а теснотой связи между ними.

Общая схема построения адаптивных моделей выглядит следующей. По нескольким первым уровням ряда оцениваются значения параметров модели. По выбранной модели строится прогноз на один шаг вперед. Отклонение прогноза от наблюдаемого уровня считается ошибкой и используется для корректировки модели.

Скорректированная модель используется для прогноза на следующем шаге и т.д. В результате к концу исследуемого интервала времени модель «обучаясь» таким образом отражает тенденцию развития процесса, имеющую место в данный момент.

В практике прогнозирования в большинстве случаев используют две СС-модели – Брауна и Хольта. Эти модели представляют процесс развития как линейную тенденцию с постоянно изменяющимися параметрами. Они относятся к схеме скользяшего среднего, используют также модель авторегрессии.

Мультипликативная модель аналогична аддитивной модели с той лишь разницей, что рассчитанные по линейной модели значения корректируются путем их умножения на сезонные коэффициенты.

Прогноз на 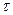шагов строиться по формуле: 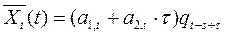,. (3.1.1)

а модификация параметров производится по соотношениям:

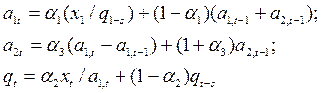(3.1.2)

где: q – фактор сезонности,

s – период сезонности,

a_1t, a_2t – текущие коэффициенты адаптивного полинома,

α₁, α₂ – параметры сглаживания.

Для более точного отображения процессов с сильной сезонностью может использоваться специальная процедура корректировки параметра сглаживания уровня процесса.

Для несезонных временных рядов вычислительные формулы упрощаются за счет исключения сезонной компоненты. При построении модели производится численная оптимизация параметров адаптации в пределах [0;1].

Прогнозирование временных рядов предназначено для формирования на основе математической модели точечного и интервального прогнозов исследуемого показателя и выдачи пользователю степени доверия к полученным результатам. В качестве классов моделей используются кривые роста, адаптивные модели Брауна и Хольта, Бокса-Дженкинса (модели авторегрессии АР(р) порядка р) и ОЛИМПа (модели АРСС(p,q,d) порядка р и скользящего среднего порядка q, порядка разностного оператора d). Прогноз отражается на графиках аппроксимации с указанием верхней и нижней границ, относительной и абсолютной ошибок и др.

Итогом работ по выбору математической модели прогноза является формирование ее обобщенных характеристик: вида уравнения регрессии и значение его параметров; оценки точности и адекватности модели; прогнозные оценки: точечные и интервальные.

2.Экспоненциальное сглаживание.

Экспоненциальное сглаживание заключается в том, что в процедуре нахождения сглаженного уровня используются значения только предшествующих уровней ряда, взятые с определенным весом, причем вес наблюдения уменьшается по мере удаления его от момента времени, для которого определяются сглаженные значения уровня ряда. Если для исходного временного ряда у₁,у₂,…,у_n соответствующие сглаженные значения уровней обозначить через S_t, t= 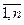, то экспоненциальное сглаживание осуществляется по формуле:

S_t = αy_t +(1-α) S_t-1 (3.2.1)

где: α – параметр сглаживания (0<α<1),

(1-α) – коэффициент дисконтирования.

Используя данную формулу для всех уровней ряда, начиная с первого и, включая момент времени t, можно получить экспоненциальное среднее, т.е. сглаженное значение уровня ряда, является взвешенной средней всех предшествующих уровней:

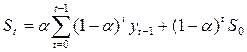, (3.2.2)

где S₀ – величина, характеризующая начальные условия.

Параметр α рекомендуется брать в интервале от 1 до 0,3. в отдельных случаях (Р.Браун) рекомендуется рассчитывать этот параметр, исходя из длины сглаживаемого ряда:

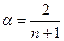(3.2.3)

Или по формуле, предложенной Мейером

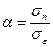, (3.2.4)

где σ_n - средняя квадратическая ошибка модели, σ_ε - средняя квадратическая ошибка исходного ряда.

Параметр S₀ принимают равным начальному уровню ряда У₁ или – средней арифметической нескольких первых членов ряда, параметр:

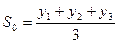(3.2.5)

Если при подходе к правому концу ряда сглаженные этим методом значения при выбранном параметре α начинают резко отличаться от соответствующих значений исходного ряда, необходимо перейти на другой параметр сглаживания.

Метод экспоненциального сглаживания является одним из наиболее эффективных, надежных и широко применяемых методов прогнозирования. Он позволяет получить оценку параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения, и при этом отличается простотой вычислительных операций.

Метод экспоненциального сглаживания применяется для прогнозирования нестационарных временных рядов, имеющих случайные изменения уровня и угла наклона, и известен под названием метода Брауна.

В качестве основной модели ряда рассматривается его локальная аппроксимация в виде полинома невысокой степени p:

x (t) = a₀ (t) + a₁ (t) t + a₂ (t) t ² +...+ a_p (p) t ^p + h, (3.2.6)

коэффициенты которого a_i медленно меняются со временем.

.

Модификацией метода экспоненциального сглаживания для сезонных рядов являются методы Уинтерса и Тейла-Вейджа (Тейл, 1971). В качестве модели ряда используется его представление в виде комбинации линейного тренда с сезонной составляющей, наложенной либо мультипликативно (модель Уинтерса), либо аддитивно (модель Тейла - Вейджа). Предполагается, что коэффициенты тренда и сезонная составляющая могут медленно меняться во времени. В соответствии с этим вычислительный процесс устроен как адаптивная процедура, управляемая тремя параметрами адаптации (один параметр - адаптация уровня, второй - угла наклона, третий - коэффициентов сезонности). Каждый параметр должен находится в интервале от 0 до 1: чем ближе параметр к единице, тем больший вес приписывается последним наблюдениям. В ходе вычислений строится сглаженный ряд, представляющий собой в каждый момент времени t прогноз по данным до момента (t -1) включительно.

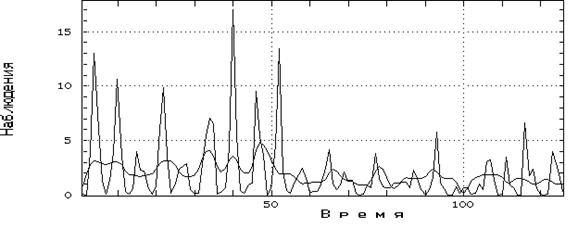
Результаты сезонного экспоненциального сглаживания ряда NCAL (аддитивная модель) и ряда NROT (мультипликативная модель) при l = 6 представлены соответственно на рис. 3.2.2 и 3.2.3.

Рис.3.2.2 Результаты сезонного экспоненциального сглаживания ряда NCAL (аддитивная модель)

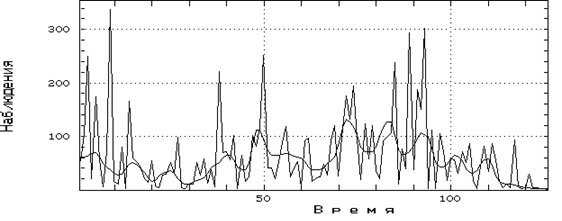Рис.3.2.3 Результаты сезонного экспоненциального сглаживания ряда NROT (мультипликативная модель)

3.Авторегрессионные модели

Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Например, потребление в момент времени t (формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например потребления в период t-1. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии.

Построение моделей авторегрессии имеет свою специфику. Во-первых, оценка параметров моделей авторегрессии не может быть проведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов. Во-вторых, исследователям приходиться решать проблемы выбора оптимальной величины лага и определения его структуры. В-третьих, между моделями авторегрессии и моделями с распределенным лагом имеется определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.

Пусть имеется следующая модель:

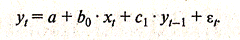(3.3.3)

Как и в модели с распределенным лагом, b₀ в этой модели характеризует краткосрочное изменение у_t под воздействием изменения х_t на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные, К моменту времени t+1 результат у_t изменился под воздействием изменения изучаемого фактора в момент времени t на b₀ единиц, а у_t+1 - под воздействием своего изменения в непосредственно предшествующий момент времени на с₁ единиц. Таким образом, общее абсолютное изменение результата в момент t+1 составит b₀с₁ единиц. Аналогично в момент времени t +2 абсолютное изменение результата составит b₀с₂ единиц и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточного мультипликаторов:

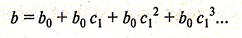(3.3.4)

Учитывая, что практически во все модели авторегрессии вводится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной у_t-1 по абсолютной величине меньше единицы |c₁|< 1, соотношение (3.3.3) можно преобразовать следующим образом:

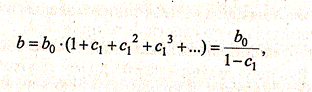(3.3.5)

где |c₁|< 1.

Такая интерпретация коэффициентов модели авторегрессии, и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.

Например: Предположим, по данным о динамике показателей потребления и дохода в регионе была получена модель авторегрессии, описывающая зависимость среднедушевого объема потребления за год (С, млн. у.е.) от среднедушевого совокупного годового дохода (У, млн. у.е.) и объема потребления предшествующего года:

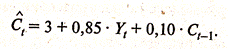(3.3.6)

Краткосрочный мультипликатор равен 0,85. В этой модели он представляет собой предельную склонность к потреблению в краткосрочном периоде. Следовательно, увеличение среднедушевого совокупного дохода на 1 млн. у.е. приводит к росту объема потребления в тот же год в среднем на 850 тыс.у.е. Долгосрочную предельную склонность к потреблению в данной модели можно определить в соответствии с формулой (1.3) как

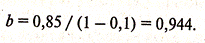
В долгосрочной перспективе рост среднедушевого совокупного дохода на 1 млн у.е. приведет к росту объема потребления в среднем на 944 тыс. у.е. Промежуточные показатели предельной склонности к потреблению можно определить, рассчитав необходимые частные суммы за соответствующие периоды времени. Например, для момента времени t+1 получим:

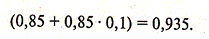
Это означает, что увеличение среднедушевого совокупного дохода в текущем периоде на 1 млн. у.е. ведет к увеличению объема потребления в среднем на 935 тыс.у.е. в ближайшем следующем периоде.

При построении моделей авторегрессии возникают две серьезные проблемы:

Первая проблема связана с выбором метода оценки параметров уравнения авторегрессии. Наличие лаговых значений результативного признака в правой части уравнения приводит к нарушению предпосылки МНК о делении переменных на результативную (стохастическую) и факторные (нестохастические).

Вторая проблема состоит в том, что поскольку в модели авторегрессии в явном виде постулируется зависимость между текущими значениями результата у_t и текущими значениями остатков u_t, очевидно, что между временными рядами y_t-1 и u_t-1 также существует взаимозависимость. Тем самым нарушается еще одна предпосылка МНК, а именно предпосылка об отсутствии связи между факторным признаком и остатками в уравнении регрессии. Поэтому применение обычного МНК для оценки параметров уравнения авторегрессии приводит к получению смещенной оценки параметра при переменной y_t-1.

Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки МНК, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Применительно к моделям авторегрессии необходимо удалить из правой части модели переменную y_t-1 Искомая новая переменная, которая будет введена в модель вместо y_t-1 должна иметь два свойства. Во-первых, она должна тесно коррелировать с y_t-1, во-вторых, она не должна коррелировать с остатками u_t.

Существует несколько способов получения такой инструментальной переменной. Поскольку в модели (3.3.3) переменная у_t зависит не только от у_t-1, но и от х_t, можно предположить, что имеет место зависимость у_t-1 от х_t-1, т. е.

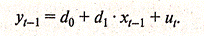(3.3.7)

Следовательно, переменную у_t-1 можно выразить следующим образом:

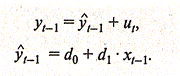(3.3.8, 3.3.9)

Найденная с помощью уравнения (3.3.7), параметры которого можно искать обычным МНК, оценка 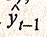может служить в качестве инструментальной переменной для фактора у_t. Эта переменная, во-первых, тесно коррелирует с у_t-1, во-вторых, как показывает соотношение (3.3.7), она представляет собой линейную комбинацию переменной х_t-1, для которой не нарушается предпосылка МНК об отсутствии зависимости между факторным признаком и остатками в модели регрессии. Следовательно, переменная также не будет коррелировать с ошибкой u_t.

Таким образом, оценки параметров уравнения (3.3.3) можно найти из соотношения

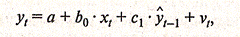(3.3.10)

предварительно определив по уравнению (3.3.7) расчетные значения у_t-1.

Допустимо использовать также следующую модификацию этого метода. Подставим в модель (3.3.3) вместо у_t-1 его выражение из уравнения (3.3.5):

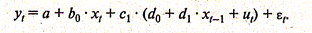(3.3.11)

Получим следующую модель:

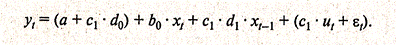(3.3.12)

Уравнение (3.3.13) представляет собой модель с распределенным лагом, для которой не нарушаются предпосылки обычного МНК, приводящие к несостоятельности и смещенности оценок параметров. Определив параметры моделей (3.3.5) и (3.3.12), можно рассчитать параметры исходной модели (3.3.3) а, b₀ и с₁.

Модель (3.3.12) демонстрирует еще одно важное свойство изложенного выше метода инструментальных переменных для оценки параметров моделей авторегрессии: этот метод приводит к замене модели авторегрессии на модель с распределенным лагом.

Отметим, что практическая реализация метода инструментальных переменных осложняется появлением проблемы мультиколлинеарности факторов в модели (3.3.7): функциональная связь между переменными 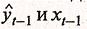приводит к появлению высокой корреляционной связи между переменными 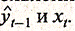В некоторых случаях эту проблему можно решить включением в модель (3.3.7) и соответственно в модель (3.3.3) фактора времени в качестве независимой переменной.

Еще один метод, который можно применять для оценки параметров моделей авторегрессии типа (3.3.3), — это метод максимального правдоподобия.

При оценке достоверности моделей авторегрессии необходимо учитывать специфику тестирования этих моделей на автокорреляцию остатков. Для проверки гипотез об автокорреляции остатков в моделях авторегрессии нельзя использовать критерий Дарбина—Уотсона. Это объясняется тем, что применение критерия Дарбина—Уотсона предполагает строгое соблюдение предпосылки о разделении переменных модели на результативную и факторные (точнее — о нестохастической природе факторных признаков уравнения регрессии). При наличии в правой части уравнения регрессии лаговых значений результата и, следовательно, несоблюдении этой предпосылки фактическое значение критерия Дарбина—Уотсона приблизительно равно двум как при отсутствии, так и при наличии автокорреляции остатков. Происходит это по следующей причине.

Предположим, в уравнении (3.3.3) имеет место автокорреляция остатков, т. е.

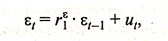(3.3.13)

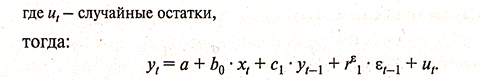(3.3.14)

Для периода t-1 уравнение (3.3.3) примет вид:

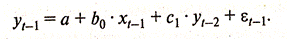(3.3.15)

Как следует из соотношения (3.3.15), переменные y_t-1 и с₁ взаимосвязаны. Поэтому в соотношении (3.3.13) часть воздействия ε_t-1 на у_t будет объясняться взаимодействием y_t-1 и поэтому чистое воздействие на у_t будет невелико. Критерий Дарбина—Уотсона в данной ситуации будет в основном характеризовать случайные остатки u_t, а не остатки с₁ в модели (3.3.3).

Для проверки гипотезы об автокорреляции остатков в моделях авторегрессии Дарбин предложил использовать другой критерий, который называется критерием h Дарбина. Его расчет проводится по следующей формуле:

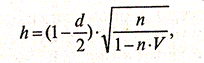(3.3.16)

Распределение этой величины приблизительно можно аппроксимировать стандартизованным нормальным распределением. Поэтому для проверки гипотезы о наличии автокорреляции остатков можно либо сравнивать полученное фактическое значение критерия h с табличным, воспользовавшись таблицами стандартизованного нормального распределения, либо действовать в соответствии со следующим правилом принятия решения.

1. Если h> 1,96, нулевая гипотеза об отсутствии положительной автокорреляции остатков отклоняется

2. Если h <—1,96, нулевая гипотеза об отсутствии отрицательной автокорреляции остатков отклоняется.

3. Если —1,96 <h < 1,96, нет оснований отклонять нулевую гипотезу об отсутствии автокорреляции остатков.

4. Модели скользящего среднего.

Для выявления аномальных уровней временных рядов используются следующие методы, рассчитанные для статистических совокупностей: метод Ирвина, метод проверки разностей средних уровней, метод Фостера – Стьюарта.

Как правило, уровни рядов динамики колеблются и, как следствие, тенденция изменения ряда получается скрытой.

С целью выявления тенденции изменения экономического ряда динамики для применения методов прогнозирования с помощью трендовых моделей, необходимо провести сглаживание (выравнивание) временного ряда.

Методы сглаживания экономических рядов динамики делятся на следующие две группы:

1. Аналитическое выравнивание с использованием кривой проведенной между конкретными уровнями ряда, определяющую основную тенденцию изменения ряда и освобождающую его от незначительных колебаний.

2. Механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней.

До «работы» с временным рядом необходимо провести предварительный анализ. Он заключается в выявлении и устранении аномальных значений уровней ряда, а также в определении наличия тренда. Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и, которое, оказывает существенное влияние на значения основных характеристик ряда, в том числе на соответствующую трендовую модель. При наличии аномальных наблюдений могут быть ошибки технического порядка или ошибки первого и второго рода. Ошибки первого рода возникают при агрегировании и дезагрегировании показателей, при передаче информации и по другим причинам. Они подлежат выявлению и устранению.

К ошибкам второго рода относят аномальные уровни, которые могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющийся эпизодически, редко. Эти ошибки устранению не подлежат.

Самым простым методом механического сглаживания является метод простой скользящей средней.

Для временного ряда у₁, у₂, у₃,…у_n определяется интервал сглаживания т (т <n).

Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания необходимо брать по возможности большим. Интервал сглаживания уменьшают, если необходимо сохранить более мелкие колебания. При прочих равных условиях интервал сглаживания рекомендуется брать нечетным.

Для первых т уровней временного ряда вычисляется их средняя арифметическая. Она отражает сглаженное значение уровня ряда, находящегося в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление средней арифметической и т.д.

Для вычисления сглаженных уровней ряда 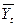используется следующая формула:

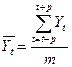, t>р (3.4.1)

где 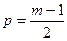(при нечетном т);

для четных т формула усложняется.

В результате такой процедуры получается n-m+1 сглаженных значений уровней ряда. При этом первая р и последняя р уровней ряда теряются (не сглаживаются). Данный метод применим для рядов, имеющих линейную тенденцию.

Метод взвешенной скользящей средней заключается в том, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Это связано с тем, что аппроксимация ряда в пределах интервала сглаживания осуществляется с использованием полинома не первой степени, как в предыдущем случае, а степени, начиная со второй.

Используется формула средней арифметической взвешенной:

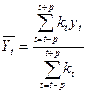, (3.4.2)

Причем веса k_t определяются с помощью метода наименьших квадратов. Эти веса рассчитаны для различных степеней аппроксимирующего полинома и различных интервалов сглаживания. Так для полиномов второго и третьего порядков числовая последовательность весов при интервале сглаживания т =5 имеет вид: {-3;12;17;12;-3}, а при т =7 - {-2;3;6;7;6;3;-2}.

Для полиномов четвертой и пятой степени и при интервале сглаживания т =7 последовательность весов следующая: {5;-30;75;131;75;-30;5}.

5. Интегрированные процессы. Идентификация авторегрессионной модели скользящего среднего.

При использовании модели авторегрессии одной из проблем является необходимость экономии параметров. Для этого в модель регрессии включают одновременно индикаторы авторегрессии и скользящего среднего.

В целом авторегрессионные модели и модели скользящего среднего известны относительно давно, но их использование в моделировании временных рядов затруднялось из-за отсутствия соответствующих методов идентификации, оценивания и контроля этих моделей, наличия неадекватных методов для описания нестационарных рядов. При формализации нестационарных рядов используют классы моделей, которые пригодны для представления широкого диапазона практических ситуаций, т.е. использую конечные разности порядка d:

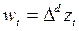. (3.5.1)

Конечная разность первого порядка имеет вид: DZ_t=Z_t – Z_t-1.

Стационарный ряд можно затем представить с помощью АРСС – модели:

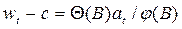, (3.5.2)

где z_t, z_t-1 – значение предварительно преобразованной переменной;

a_t – процесс «белого шума»;

В – оператор сдвига назад;

j (В) – функция оператора сдвига (параметр авторегрессии);

q - параметр скользящего среднего.

Данная модель называется авторегрессионной интегрированной моделью скользящего среднего.

Взаимосвязанная статистически методика метода Бокса-Дженкинса включает: а) идентификация временного ряда (т.е. определение размерностей операторов конечной разности, авторегрессии и скользящего среднего); б) оценивание параметров модели; в) проверка адекватности модели.

Сезонная модель Бокса-Дженкинса содержит сезонные операторы конечной разности, авторегрессии и скользящего среднего. В операторном виде она приобретает следующий вид:

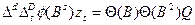, (3.5.3)

где s – период сезонности;

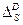- оператор сезонной конечной разности

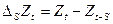(3.5.4)

где D – порядок сезонной конечной разности;

f - оператор сезонной авторегрессии порядка р;

q - оператор сезонного скользящего среднего порядка Q;

d f,Q – определенные значения.

Модель называется сезонной моделью авторегрессии – скользящего среднего (рхdxq)x(P,D,Q).

Основные этапы разработки сезонной модели аналогичны этапам для несезонной модели.

Для моделирования нестационарных временных рядов используется метод ОЛИМП, который является распространенной моделью авторегрессии скользящего среднего.

Если идентифицированная модель Бокса-Дженкинса с параметрами р, d, q, то соответствующая модель ОЛИМП должна иметь параметры: p^/ = p+d. Если процесс удовлетворяет стохастическому разностному уравнению порядка р (авторегрессионный процесс):

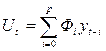, (3.5.5)

где ф_i – коэффициент оператора автрорегрессии;

U_i – последовательность независимых одинаково распределенных случайных величин с дисперсией s²_е, t=0,1,…,t, известны начальные значения у-р, у-р+1,…,у-1, то прогноз может выражаться следующим образом:

Е(y_t|y_t-1,…,y₀)= 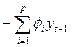, (3.5.6)

где Е – оператор математического ожидания.

6.Доверительные интервалы прогноза.

После проверки всех моделей прогнозирования из выбранного массива на адекватность необходимо выполнить оценку их точности.

Наиболее часто на практике используют следующие характеристики: оценка стандартной ошибки; средняя относительная ошибка оценки; среднее линейное отклонение; ширина доверительного интервала в точке прогноза.

Для получения последней статистической оценки определяется доверительный интервал в прогнозируемом периоде, т.е. возможные отклонения прогноза от основной тенденции протекания рассматриваемого процесса. В основе доверительного интервала лежат интервальные оценки параметров регрессии а₀ и а₁:

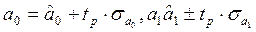, (3.5.7)

Где 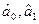- точечные оценки (середины интервалов), рассчитанные с помощью метода наименьших квадратов;

t_p – теоретическое значение критерия Стьюдента при уровне значимости, равном 5% и числе степеней свободы, равном j=n-m-1;

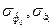- стандартные ошибки коэффициентов регрессии, вычисляемые по следующим формулам:

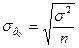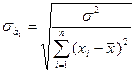; ; (3.5.8)

s² – несмещенные оценки дисперсии случайной составляющей:

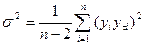, (3.5.9)

где х_i, y_i – фактические значения динамических рядов х, у;

у_ti - теоретическое значение, рассчитанное по уравнению регрессии;

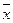- среднее значение фактора х.

Верхняя Y_B и нижняя Y_Н границы доверительного интервала будут равны:

Y_B = f(a₀^B; а₁^В; х_n); (3.5.10)

Y_Н = f(a₀^Н; а₁^Н; х_n), (3.5.11)

Где a₀^B, a₀^Н – верхнее и нижнее значение параметра а₀ модели прогноза;

а₁^В , а₁^Н – верхнее и нижнее значение параметра а₁ модели прогноза;

х_n – значение фактора времени в точке прогноза.

Ширина доверительного интервала будет равна:

D=Y^B – Y^Н. (3.5.12)

Ширина доверительного интервала зависит:

- от числа степеней свободы и тем самым от объема выборки, т.е. чем больше объем выборки, тем меньше (при прочих равных условиях) значение критерия Стьюдента (t) и, следовательно, уже доверительный интервал;

- от величины стандартной ошибки оценки параметра регрессии (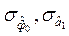). Чем меньше 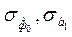, тем меньше при прочих равных условиях ширина доверительного интервала.

Лучшей по точности считается та модель, у которой все перечисленные характеристики имеют меньшую величину. Однако эти показатели по разному отрицают степень точности модели и поэтому нередко дают противоречивые выводы. Для однозначного выбора лучшей модели необходимо использовать либо один основной показатель, либо обобщенный критерий.

7. Предсказание доходности и волатильности на финансовых рынках.

В сущности, волатильность - это мера неопределенности инвестиции. Любое движение цены может быть разбито на две части: 1) ожидаемое движение цены и 2) движение, которое мы не ожидали.

Ожидаемая (не волатильная) часть движения цены инвестиции обычно описывается понятием «Ожидаемой ставки доходности» (expected growth rate). На коротком промежутке времени большинство инвесторов "предсказывают" будущую норму доходности исходя из недавней модели поведения роста цены. Обычной мерой, используемой для описания ставки (нормы) доходности является среднегеометрическая ставка доходности или CAGR. На рисунке 3.9.1 центральная светло-красная линия показывает "ожидаемый" инвестором рост цены инвестиции, которая была приобретена по $10 и удерживалась 12 месяцев.

Не ожидаемая часть движения цены инвестиции и есть ее волатильность. Эта часть может, как расти, так и падать с равной вероятностью, т.к. по определению она не предсказуема. Ввиду нашей неопределенности относительно движения цены, существует вероятность распределения цен вокруг своей "ожидаемой" цены. Это распределение вероятности лежит в основе концепции "волатильности". Описывая его форму и размер, мы, по сути, описываем волатильность. На рисунке 3.9.1 вероятность каждой конечной цены инвестиции показана цветом. Шкала цвета начинается от голубого (наименее вероятно) цвета через пурпурный и красный до желтого (наиболее вероятно) цвета.

Цветная гистограмма показанная на рисунке 3.9.1 основана на 25000 независимых испытаниях вымышленных инвестиций, чьи годовые нормы доходности равны 100% с очень высокой волатильностью. Эффект воздействия высокой волатильности очень четко показан на рисунке 3.9.1: некоторые инвесторы могли видеть доходность выше 600%, в то время как другие могли потерять более 60% вложений. Следовательно, первоначальная неопределенность инвесторов относительно результата своих вложений на самом деле очень высокая.

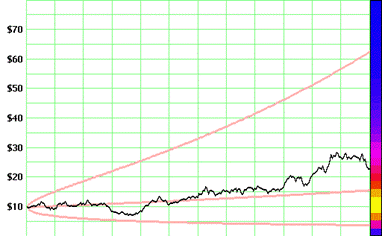
Рисунок 3.9.1. Движения цена за 12 месяцев с вероятностным распределением справа. Свело-красные линии показывают конверт из 2-х сигм, в рамках которых цена будет колебаться.