2015-10-13
376
План:
1. Компоненты временного ряда.
2. Выделение тренда.
3. Моделирование сезонных и циклических колебаний.
4. Сглаживание временных рядов.
5. Динамические модели с распределенными лагами.
6. Стационарные временные ряды.
7. Тестирование стационарности.
8. Коинтеграция временных рядов..
1. Компоненты временного ряда.
Экономическая модель строится с использованием двух типов исходных данных: данные, характеризующие совокупность различных объектов в определенный момент (период) времени; данные, характеризующие один объект за ряд последовательных моментов (периодов) времени. Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.
Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени (в литературе используются синонимы этого термина – динамический ряд и ряд динамики).
Составными элементами рядов динамики являются числовые значения исследуемого показателя, называемые уровнями этих рядов и моменты или интервалы времени к которым относятся эти уровни.
Ряды динамики, состоящие из показателей характеризующих экономическое явление в определенные моменты времени, называются моментными (например, ежедневный остаток товаров фирмы на складе по состоянию на 22 часа.)
Если численные значения показателя (уровни) представляют собой сумму за определенный период, то динамический ряд называется интервальным (например, объемы продаж фирмы по кварталам года).
Временной ряд характеризуется также длиной. Длина временного ряда – это время или число уровней, прошедшее от начального до конечного момента. Так, например, длина времени ряда во втором примере равна одному году или четырем кварталам.
Если ряд динамики имеет устойчивую длительную тенденцию, то говорят, что имеет место тренд. Следовательно, тренд показывает основную тенденцию изменения временного ряда. Математическая модель экономической системы, развитие которой отображается через тренд называется трендовой моделью.
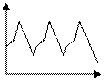
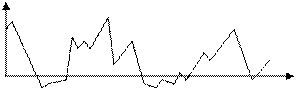
При различных сочетаниях этих факторов в изучаемом явлении или процессе зависимость уровней ряда от времени может принимать различные формы: 1) Большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя (рис. 1а - временной ряд, содержащий возрастающую тенденцию; 2) Изучаемый показатель может быть подвержен циклическим колебаниям (рис. 1б); 3) Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой случайной компоненты (рис. 1в).
Реальные данные, чаще всего, содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент.
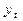
t t t
а) возрастающая б) сезонная в) случайная компонента
тенденция компонента
Рисунок 1 – Основные компоненты временного ряда
Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда.
Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативноймоделью временного ряда.
Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Формула для расчета коэффициента корреляции:
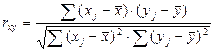(2.1.1).
Коэффициент автокорреляции уровней первого порядка, который измеряет зависимость между соседними уровнями ряда t и t -1 (т.е. при лаге 1):
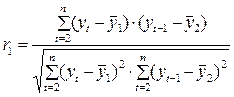, где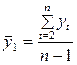 
, 
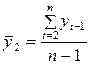(2.1.2)
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
Отмечают два важных свойства коэффициента автокорреляции: 1) коэффициент автокорреляции строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию, коэффициент автокорреляции уровней исходного ряда может приближаться к нулю; 2) по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка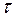 
, ряд содержит циклические колебания с периодичностью в 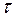моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. в, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты (Т) и циклической (сезонной) компоненты (S).
2. Выделение тренда.
Трендовые модели, как было отмечено выше, – это модели, определяющие общее направление развития, основную тенденцию (тренд) временных рядов (рядов динамики). Прогнозирование на основе рядов динамики относится к одномерным методам прогнозирования и основывается на экстраполяции (продление сложившейся тенденции на будущее).
Использование метода экстраполяции на основе кривых роста исходит из следующих посылок:
- ряд динамики действительно имеет тенденцию развития (тренд);
- условия, определяющие тренд не изменяются в будущем.
Существует два основных класса трендовых моделей – параметрические и непараметрические.
В параметрических моделях в основании ряда предполагается определяющая закономерность, которая может быть выявлена кривой, проведенной между уровнями временного ряда освобождая их от отклонений, вызываемых мелкими волнами и беспорядочными колебаниями. Параметры в уравнении такой кривой остаются неизменными на протяжении всего ряда. Процедура определения тренда по параметрической модели называется выравниванием.
Непараметрические методы основаны на определении отдельных точек ряда с помощью групп соседних (предшествующих и последующих) членов ряда, составляющих активную окрестность (интервал скольжения, период усреднения). Метод построен так, что при выявлении тренда в отдельных его точках не должен искажаться вид тренда в пределах активной окрестности, а вместе с тем, чтобы взаимодействием соседних членов ряда погашались бы беспорядочные искажения тренда. Процедура определения тренда по непараметрической модели называется экспоненциальнымсглаживанием.
Наличие либо отсутствие тренда часто хорошо видно на графике. Проверку этой гипотезы в сомнительных случаях можно осуществить с использованием некоторых простых критериев, широко описанных в литературе по статистике. Приведем некоторые из них.
Тест числа поворотных точек основан на вычислении числа локальных максимумов. Отклонение этого числа от идеального значения (Юл, Кендал, 1960; Вайну, 1977) в большую сторону свидетельствует о значительной дисперсии и заметной отрицательной автокорреляции случайной компоненты. Отклонение в меньшую сторону может возникнуть как при наличии тренда, так и в случае положительной автокорреляции (первого порядка) случайной компоненты. Последняя ситуация возникает и для стационарных рядов.
Критерий знаков разности чувствителен как к наличию тренда, так и к присутствию квазипериодической компоненты. Случайная компонента мало сказывается на результатах тестирования с использованием этого критерия.
Критерий ранговой корреляции Кендала является хорошим тестом на наличие монотонного или кусочно-монотонного тренда для не очень длинных рядов. Положительный коэффициент соответствует возрастающему тренду, отрицательный - убывающему.
Критерий ранговой корреляции Спирмена по своему смыслу и свойствам близок к коэффициенту Кендала.
 |
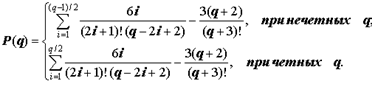Недостатком непосредственного использования описанных методов является необходимость большого числа наблюдений, что трудно реализуемо в экологическом исследовании. При сравнительно малом числе наблюдений (чаще всего менее 30) целесообразно использовать, например, иную методику проверки случайного характера распределения числа поворотных точек (Розенберг, Рудерман, 1969; Розенберг, 1984), которую Н.Ф.Реймерс (1990) назвал "принципом скользящих среднемаксимальных случайного статистического ряда". Не ставя задачей воспроизвести все выкладки, лежащие в основе полученных законов распределений, приведем лишь окончательный результат: вероятность P (q) того, что число наблюдений между соседними точками максимума (для реализации непрерывной случайной величины с произвольным законом распределения) равно q:
Необходимо подчеркнуть два интересных свойства данного закона распределения: независимость этого распределения от функции распределения исходной случайной величины (иными словами, значительная общность данного закона распределения) и строгое равенство математического ожидания M (q)=3 (последний вывод совпадает с оценкой Дж.Юла и М.Кендала; 1960). Таким образом, распределение вероятности получения "расстояния" q между соседними поворотными точками типа максимума имеет вид:
Таблица 2.2.1 – Распределение вероятностей
| q | |||||||
| P (q) | 0.4000 | 0.3333 | 0.1714 | 0.0667 | 0.0212 | 0.0057 | 0.0013 |
Следовательно, сама случайная природа любого (!) временного ряда может стать причиной объявления "циклических" изменений (вероятность циклов в два, три и четыре наблюдения оказывается больше 0,9). Такого рода ситуация является еще одним примером возникновения "ложной корреляции". Интересно отметить и тот факт, что данный закон получен при независимых наблюдениях над случайной величиной, т.е. влияние каких-либо субъективных факторов заведомо исключено.
