Методика построения доверительных интервалов для параметра q распределения вероятностей:
1) из генеральной совокупности значений случайной величины X, имеющей функцию распределения F (x, q), извлекается выборка объема n;
2) по результатам выборки находится точечная оценка 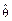 параметра q распределения вероятностей;
параметра q распределения вероятностей;
3) составляется вспомогательная случайная величина 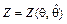 , закон распределения вероятностей
, закон распределения вероятностей 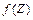 которой известен;
которой известен;
4) задается доверительная вероятность 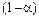 ;
;
5) используя плотность распределения вероятностей 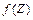 случайной величины Z, находят такие два числа Z 1 и Z 2 (рисунок 1), что
случайной величины Z, находят такие два числа Z 1 и Z 2 (рисунок 1), что
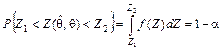 ; (1)
; (1)
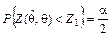 ;
; 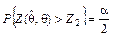 ;
;
6) как только Z 1 и Z 2 найдены, двойное неравенство 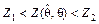 решается относительно q и получается искомый интервал
решается относительно q и получается искомый интервал 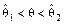 .
.
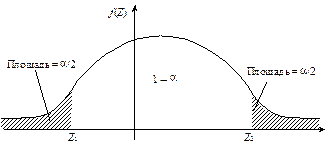
Рисунок 1 – Двусторонняя критическая область статистического критерия
3 Доверительные интервалы для математического ожидания
и дисперсии случайной величины,
имеющей нормальное распределение
Пусть вероятностный эксперимент описывается случайной величиной X и известно, что X подчиняется нормальному закону распределения вероятностей
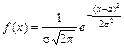 ,
, 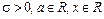 ,
,
где 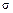 – среднее квадратическое отклонение случайной величины X, причем значения a и
– среднее квадратическое отклонение случайной величины X, причем значения a и 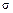 нам неизвестны;
нам неизвестны;
Построим доверительный интервал 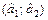 для неизвестного значения a математического ожидания. Воспользуемся алгоритмом, изложенным в пункте 2:
для неизвестного значения a математического ожидания. Воспользуемся алгоритмом, изложенным в пункте 2:
1) извлечем выборку 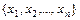 объема n из генеральной совокупности;
объема n из генеральной совокупности;
2) по выборке найдем точечные оценки параметров a и 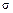 :
:
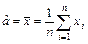 ,
, 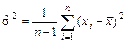 ;
;
3) составим случайную величину
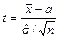 . (2)
. (2)
Доказано, что случайная величина t имеет распределение Стьюдента с 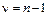 степенями свободы;
степенями свободы;
4) зададим доверительную вероятность 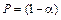 ;
;
5) найдем t 1 и t 2 такие, что
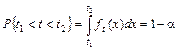 , (3)
, (3)
где 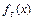 – плотность распределения Стьюдента, график которой изображен на рисунке 2.
– плотность распределения Стьюдента, график которой изображен на рисунке 2.
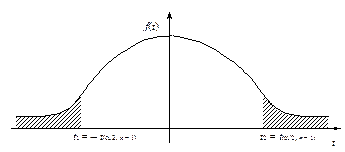
Рисунок 2 – Плотность распределения Стьюдента
Поскольку кривая плотности распределения Стьюдента симметрична относительно вертикальной оси, мы можем выражение (3) записать так
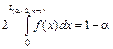 ,
,
пользуясь таблицей значений t -распределения (приложение Б), найдем значение 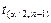 ;
;
6) полагая известными значения 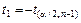 и
и 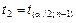 , запишем из (3) выражение в скобках
, запишем из (3) выражение в скобках
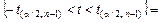 (подставим выражение для t из (2)) =
(подставим выражение для t из (2)) =
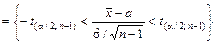 .
.
Решим двойное неравенство относительно a:
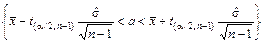 . (4)
. (4)
Таким образом, мы построили доверительный интервал (4) для параметра a.
Для построения интервальной оценки 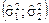 неизвестной дисперсии
неизвестной дисперсии 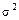 воспользуемся тем, что случайная величина
воспользуемся тем, что случайная величина 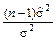 подчинена
подчинена 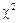 -распределению с (n – 1) степенями свободы. Поэтому
-распределению с (n – 1) степенями свободы. Поэтому
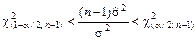 , (5)
, (5)
где 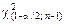 –
– 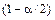 – процентная точка
– процентная точка 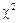 -распределения с (n – 1) степенями свободы;
-распределения с (n – 1) степенями свободы;
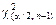 –
– 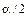 – процентная точка
– процентная точка 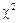 -распределения с (n – 1) степенями свободы (приложение В). Разрешая неравенство (5) относительно
-распределения с (n – 1) степенями свободы (приложение В). Разрешая неравенство (5) относительно 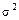 , получим случайный доверительный интервал для неизвестного параметра
, получим случайный доверительный интервал для неизвестного параметра 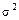
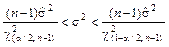 . (6)
. (6)
Соответственно доверительный интервал 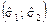 для среднего квадратического отклонения имеет вид
для среднего квадратического отклонения имеет вид
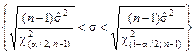 , (7)
, (7)
и таким образом мы построили доверительный интервал для параметра 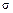 .
.
Замечание – Если случайная величина X имеет произвольную функцию распределения 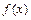 , по формулам (4) и (7) можно строить приближенные доверительные интервалы соответственно для математического ожидания и среднего квадратического отклонения, если объем выборки достаточно велик,
, по формулам (4) и (7) можно строить приближенные доверительные интервалы соответственно для математического ожидания и среднего квадратического отклонения, если объем выборки достаточно велик, 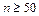 .
.
Пример 1 Из многочисленного коллектива работников фирмы случайным образом отобрано n = 25 работников. Средняя заработная плата этих работников составила 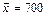 д.е. при выборочном среднеквадратическом отклонении
д.е. при выборочном среднеквадратическом отклонении 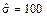 д.е. Требуется с доверительной вероятностью
д.е. Требуется с доверительной вероятностью 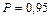 определить интервальную оценку:
определить интервальную оценку:
а) для средней месячной заработной платы на фирме;
б) суммы затрат фирмы на заработную плату отдела, состоящего из 520 сотрудников.
Решение. 1) Среднемесячная заработная плата на фирме характеризуется генеральной средней a. Требуется найти интервальную оценку 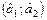 параметра a с доверительной вероятностью
параметра a с доверительной вероятностью 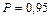 . Согласно (4) имеем
. Согласно (4) имеем
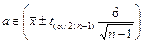 ,
,
где  –
– 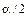 -процентная точка
-процентная точка 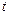 -распределения (распределения Стьюдента). По таблице (см. приложение Б) распределения Стьюдента находим
-распределения (распределения Стьюдента). По таблице (см. приложение Б) распределения Стьюдента находим 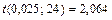 . Поэтому
. Поэтому
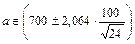 .
.
Таким образом, с вероятностью 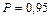 можно гарантировать, что средняя заработная плата на фирме находится в пределах:
можно гарантировать, что средняя заработная плата на фирме находится в пределах: 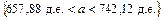 .
.
2) Средняя сумма затрат фирмы на заработную плату отдела из N сотрудников составит 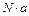 д.е. Следовательно, с вероятностью
д.е. Следовательно, с вероятностью 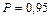 можно утверждать, что затраты фирмы на заработную плату отдела не выйдут за пределы интервала:
можно утверждать, что затраты фирмы на заработную плату отдела не выйдут за пределы интервала:
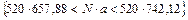 ,
,
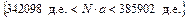 .
.
Пример 2 При анализе точности фасовочного автомата было проведено n = 24 контрольных взвешиваний пятисотграммовых пачек кофе. По результатам измерений рассчитано выборочное среднее квадратическое отклонение 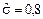 г. Требуется с доверительной вероятностью
г. Требуется с доверительной вероятностью 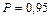 оценить точность фасовочного автомата, то есть определить интервальную оценку s.
оценить точность фасовочного автомата, то есть определить интервальную оценку s.
Решение. Согласно (6) интервальная оценка дисперсии
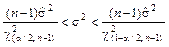 .
.
По таблице процентных точек 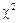 -распределения (см. приложение В) найдем
-распределения (см. приложение В) найдем
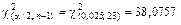 ;
;
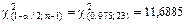 .
.
Следовательно,
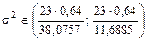 .
.
Значит с доверительной вероятностью 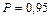 можно утверждать, что истинное значение среднего квадратического отклонения s будет находиться в интервале
можно утверждать, что истинное значение среднего квадратического отклонения s будет находиться в интервале
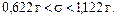
Предположив, что ошибка фасовочного автомата есть нормально распределенная случайная величина с нулевой средней и среднеквадратическим отклонением s, можно с вероятностью 0,954 утверждать, что вес пачек кофе будет в пределах
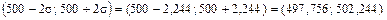 .
.
 2015-04-08
2015-04-08 3914
3914
