Статистическая термодинамика – раздел статистической физики, формулирующий законы, связывающие молекулярные свойства веществ с измеряемыми на опыте ТД величинами.
СТД посвящена обоснованию законов термодинамики равновесных систем и вычислению ТД функций по молекулярным постоянным. Основу СТД составляют гипотезы и постулаты.
В отличие от механики, в СТЛ рассматриваются средние значения координат и импульсов и вероятности появления их значений. Термодинамические свойства макроскопической системы рассматриваются как средние значения случайных величин или как характеристики плотности вероятности.
Различают классическую СТД (Максвелл, Больцман), квантовую (Ферми, Дирак, Бозе, Эйнштейн).
Основная гипотеза СТД: существует однозначная связь молекулярных свойств частиц, составляющих систему, и макроскопических свойств системы.
Ансамбль – большое, почти бесконечное число аналогичных ТД систем, находящихся в различных микросостояниях. У ансамбля с постоянной энергией все микросостояния равновероятны. Средние значения физически наблюдаемой величины за большой промежуток времени равно среднему значению по ансамблю.
§ 1. Микро- и макросостояния. Термодинамическая вероятность (статичтический вес) и энтропия. Формула Больцмана. Статистический характер второго закона ТД
Для описания макросостояния указывают небольшое число переменны (часто 2). Для описания микросостояния применяют описание конкретных частиц, для каждой из которых вводится шесть переменных.
Для графического изображения микросостояния удобно пользоваться фазовым пространством. Различают 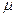 - фазовое пространство (молекулы) и Г-фазовое пространство (газ).
- фазовое пространство (молекулы) и Г-фазовое пространство (газ).
Для подсчёта числа микросостояний Больцман использовал метод ячеек, т.е. фазовый объём разбивается на ячейки, причем величина ячеек достаточно большая, чтобы поместилось несколько частиц, но маленькая по сравнению с целым объёмом.
Если полагать, что одна ячейка соответствует одному микросостоянию, то, если весь объём поделить на объём ячейки, получим число микросостояний.
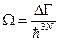
Примем, что объём фазового пространства разбит на три ячейки. Общее число частиц в системе – девять. Пусть одно макросостояние: 7+1+1, второе: 5+2+2, третье: 3+3+3. Посчитаем число микросостояний, которыми может быть реализовано каждое макросостояние. Это число способов равно 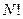 . В статистике Больцмана частицы считаются различимыми, т.е. обмен частиц между ячейками даёт новое микросостояние, но макросостояние остается тем же.
. В статистике Больцмана частицы считаются различимыми, т.е. обмен частиц между ячейками даёт новое микросостояние, но макросостояние остается тем же.
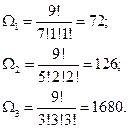
Наибольшее число микросостояний даёт система, в которой частицы равномерно распределены по всему объёму. Самое неустойчивое состояние соответствует накоплению частиц в одной части системы.
Посчитаем число микросостояний, когда число Авогадро распределено по двум ячейкам:
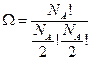
Применим формулу Стирлинга:
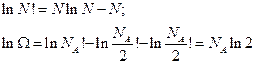
Если одна частица перескочит в чужую ячейку, получим отличие на 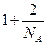 .
.
Возьмем систему, в которой произошёл переход х частиц. Пусть мы хотим, чтобы 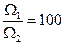 . Расчет показывает, что х = 1012.
. Расчет показывает, что х = 1012.
По мере перехода системы в равновесное состояние термодинамическая вероятность сильно растёт, энтропия тоже растёт. Следовательно, 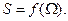
Найдём вид этой функции, для этого возьмем систему из двух ячеек. В первом случае NA+0, во втором 0,5 + 0,5. Температура постоянна. Переход от первого состояния ко второму есть изотермическое расширение газа.
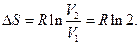
Согласно формуле Больцмана,
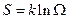
Откуда
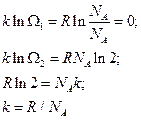
Так получается постоянная Больцмана. Теперь получим формулу Больцмана.
Возьмем две системы
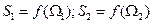
Из двух систем образуем третью, тогда энтропия новой системы будет равняться:
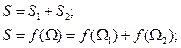
Вероятность двух независимых систем перемножается:
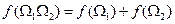
Функция логарифмическая:
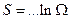
Но энтропия – величина размерная, нужен коэффициент пропорциональности. А это и есть константа Больцмана.
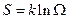
Вот здесь скользкий переход и вывод, что максимум энтропии в точке равновесия – закон не абсолютный, а статистический. Как видно, чем меньше частиц, тем реже выполняется второй закон термодинамики.
§ 2. Распределение молекул по энергии. Закон Больцмана
Система из Н частиц, 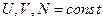 . Как молекулы распрделены по энергии? Какое число молекул обладает энергией
. Как молекулы распрделены по энергии? Какое число молекул обладает энергией 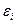 ?
?
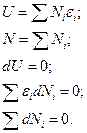
Энтропия в состоянии равновесия имеет максимальное значение:
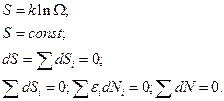
А теперь найдем что-то ещё:
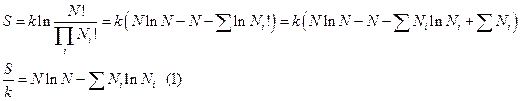
Найдём дифференциалы:
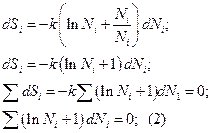
В уравнении (2) не все количества независимы
Для того, чтобы избавиться от зависимых переменных, используем метод неопределенных множителей Лагранжа:
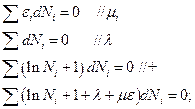
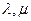 подбираются так, чтобы коэффициенты при зависимых переменных были равны нулю.
подбираются так, чтобы коэффициенты при зависимых переменных были равны нулю.
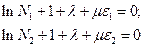
Тогда остальные члены в сумме независимы. Окончательно получится, что
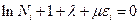
Потенцируем это уравнение:
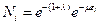 (3)
(3)
Просуммируем:
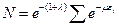 ; (4)
; (4)
 ; (5)
; (5)
Подставим в (3):
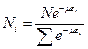 (6)
(6)
Избавимся от ещё одного множителя. Ур-е (6) логарифмируем, умножаем на 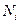 и суммируем:
и суммируем:
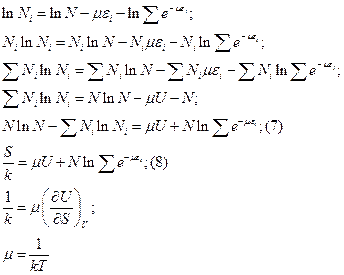
Неопределенный множитель Лагранжа стал определенным.
Окончательно, закон Больцмана запишется:
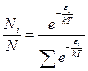
Подставим в (8) значение 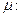
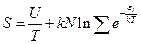 (9)
(9)
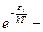 фактор Больцмана
фактор Больцмана
Иногда распределение Больцмана записывают и так:
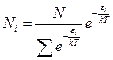
Соответственно, при температуре, близкой к абсолютному нулю, 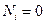 , т.е. нет молекул на возбужденных уровнях. При температуре, стремящейся к бесконечности, распределение по всем уровнями одинаково.
, т.е. нет молекул на возбужденных уровнях. При температуре, стремящейся к бесконечности, распределение по всем уровнями одинаково.
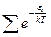 – сумма по состояниям
– сумма по состояниям
§ 3. Сумма по состояниям молекулы и её связь с термодинамическими свойствами
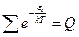
Выясним, какими свойствами обладает сумма по состояниям молекулы. Во-первых, это безразмерная величина, а её значение определяется температурой, количеством частиц и объёмом системы. Также она зависит от массы молекулы и её формы движения.
Далее, сумма по состояниям неабсолютная величина, она определена с точностью до постоянного множителя. Её величина зависит от уровня отсчёта энергии системы. Часто за этот уровень принимается температура абсолютного нуля и состояние молекулы с минимальными квантовыми числами.
Сумма по состояниям – монотонно увеличивающаяся функция температуры:
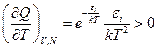
С ростом энергий 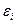 сумма по состояниям увеличивается.
сумма по состояниям увеличивается.
Сумма по состояниям молекулы обладает свойством мультипликативности. Энергию молекулы можно представить суммой поступательной и внутримолекулярной энергий. Тогда сумма по состояниям запишется так:
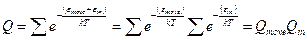
Можно ещё и так:
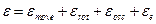
На возбуждение электронных уровней необходима высокая температура. При сравнительно невысоких температурах вклад электронных колебаний близок к нулю.
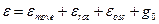
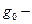 нулевой уровень электронного состояния
нулевой уровень электронного состояния
Это вот всё называется приближением Борна – Оппенгеймера.
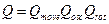
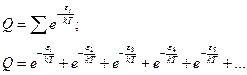
Предположим, что 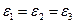 , тогда сумму можно заменить так:
, тогда сумму можно заменить так:
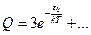
Если остальные тоже между собой практически одинаковы, то:
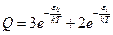
или
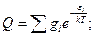
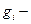 вырожденность уровней
вырожденность уровней
Такая форма записи называется суммой по энергетическим уровням молекулы.
Сумма по состояниям связана с термодинамическими свойствами системы.
Возьмем производную по температуре:
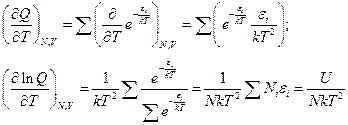
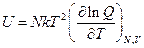
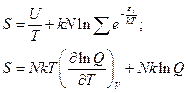
Получили выражение для энтропии
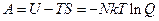
Найдем давление:
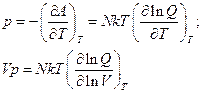
Энтальпия и энергия Гиббса:
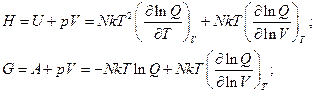
Осталась теплоемкость:
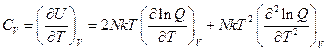
Во-первых, все величины – это приращение к нулевой энергии, во-вторых, все уравнения выполняются для систем, где частицы можно считать различимыми. В идеальном газе молекулы неразличимы.
§ 4. Каноническое распределение Гиббса
Гиббс предложил метод статистических, или термодинамических, ансамблей. Ансамбль – это большое, стремящееся к бесконечности, число аналогичных термодинамических систем, находящихся в различных микросостояниях. Микроканонический ансамбль характеризуется постонством 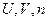 . Канонический ансамбль имеет постоянные
. Канонический ансамбль имеет постоянные 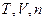 . Распределение Больцмана было выведено для микроканонического ансамбля, перейдём к каноническому.
. Распределение Больцмана было выведено для микроканонического ансамбля, перейдём к каноническому.
Какова вероятность одного микросостояния в системе в термостате?
Гиббс ввёл понятие статистического ансамбля. Представим большой термостат, поместим в него ансамбль – одинаковые системы в различных микросостояниях. Пусть М – число систем в ансамбле. В состоянии i находятся 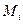 систем.
систем.
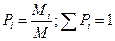
В каноническом ансамбле, поскольку могут реализоваться состояния с различной энергией, следует ожидать, что вероятности будут зависеть от уровня энергии, которому они принадлежат.
Пусть имеется состояние, где энергия системы и её энтропия равны 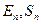 . Этой системе соответствует
. Этой системе соответствует 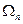 микросостояний.
микросостояний.
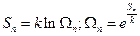
Энергия Гельмгольца всего ансамбля постоянна.
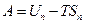
Если внутреннюю энергию приравнять к энергии 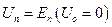 , то
, то
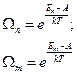
Тогда вероятность одного состояния равна
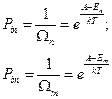
Таким образом, вероятности, относящиеся к различным энергиям, зависят от энергии системы, а она может быть различной.
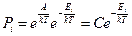 – каноническое распределение Гиббса
– каноническое распределение Гиббса
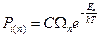 – вероятность макросостояния
– вероятность макросостояния
|

§ 5. Сумма по состояниям системы и её связь с термодинамическими функциями
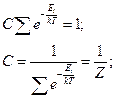
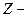 сумма по состояниям системы
сумма по состояниям системы
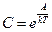
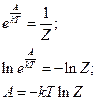
Далее:
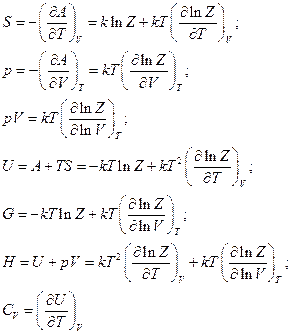
Функция состояния системы обладает свойством мультипликативности. Если энергию системы представить в виде:
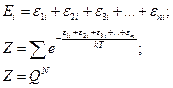
Оказалось, что эта связь действует для системы локализованных частиц. Число микросостояний для нелокализованных частиц будет гораздо меньше. Тогда:
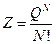
Пользуясь свойством мультипликативности, получим:
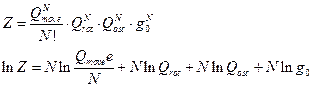
§ 6. Поступательная сумма по состояниям.
ТД свойства одноатомного идеального газа
Будем рассматривать одноатомный идеальный газ. Молекула считается точкой, которая обладает массой и способностью перемещаться в пространстве. Энергия такой частицы равна:
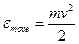
Такое движение имеет три степени свободы, поэтому представим эту энергию в виде трех составляющих. Рассмотрим движение вдоль координаты х.
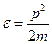
Из квантовой механики:
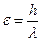
Постулируется также:
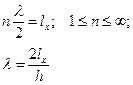
Тогда кинетическая энергия выразится так:
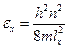
Поступательная сумма по состояниям равна:
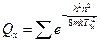
Обозначим 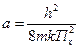 . Поскольку величины суммирования малы, заменим сумму интегралом (это также можно узаконить, если представить сумму в виде графика, в котором ступеньки различаются на очень малую величину):
. Поскольку величины суммирования малы, заменим сумму интегралом (это также можно узаконить, если представить сумму в виде графика, в котором ступеньки различаются на очень малую величину):
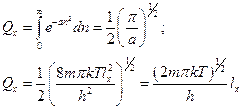
Подобные значения энергии по состояниям получим и для движения по другим осям:
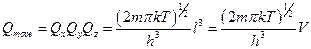
Если найдена сумма по состояниям, можно найти термодинамические функции с учетом
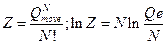
Итак,
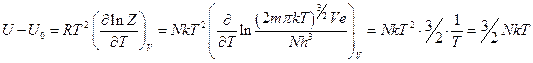
Для 1 моля газов 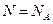 :
:
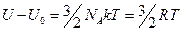
Темплоёмкость:
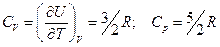
Далее,
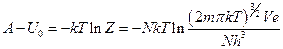
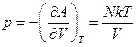 ,
,
что для 1 моля запишется:
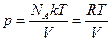 зачёт!
зачёт!
Такое чувство, будто статистическая термодинамика – интересно, если бы не способ, которым она подаётся…
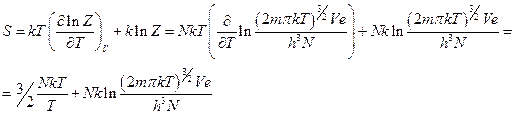
Заменим массу частным от деления молекулярной массы на число Авогадро, а объём – по уравнению состояния идеального газа:
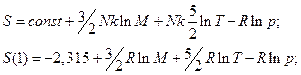
Поскольку константа задана таким числом, давление берется в атмосферах, а универсальная газовая постоянная выражается в кал / (моль К).
Из феноменологической ТД:
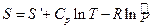 Закур – Тетрод
Закур – Тетрод
Отсюда
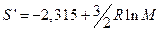
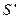 определяется молекулярной массой газа
определяется молекулярной массой газа
У него есть дети
§ 7. Вращательная сумма по состояниям жесткого ротатора

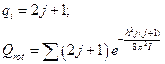
Перейдём к интегрированию:
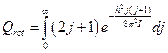
Введем новую переменную, чтобы интеграл стал табличным:
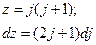
Постоянные величины обозначим ещё какой-нибудь буквой:
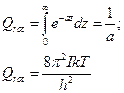
Чтобы статистические величины совпадали с эмпирическими, это все необходимо уменьшить, разделить на число симметрии:
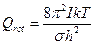
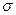 – число симметрии (одинаковых состояний при вращении молекулы на 360°)
– число симметрии (одинаковых состояний при вращении молекулы на 360°)
Число вращательных степеней свободы двухатомной молекулы равно двум.
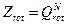
Все свойства вычисляются как по сумме состояний молекулы:
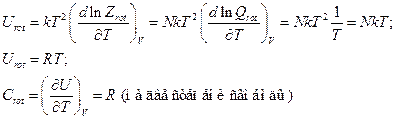
Для нелинейной молекулы
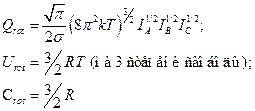
Кроме свободного вращения у молекул может наблюдаться внутреннее вращение, например, в этане происходит взаимное вращение метильных групп. Энергетический барьер для этана (разность энергий молекулы в заторможенном и заслоненном состояниях) равен 10 кДж/моль.
Выражение для внутреннего вращения:
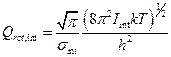
§ 8. Колебательная сумма по состояниям гармонического осциллятора.
Формула Эйнштейна
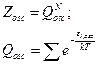
Энергия гармонического осциллятора равна:
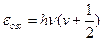
Не будем привлекать интегрирование, лучше убывающую геометрическую прогрессию:
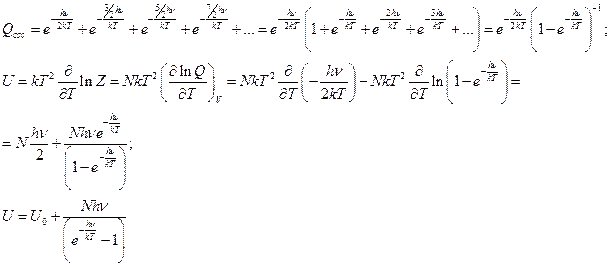
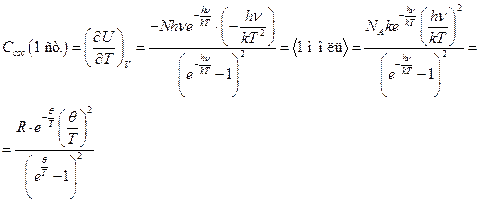
 2015-10-13
2015-10-13 3008
3008