Второй закон термодинамики

Самопроизвольные (спонтанные) процессы описываются следующими характеристиками:

1. Все природные самопроизвольные процессы протекают в одном направлении, т. е. имеют одностороннее направление. Например, тепло от горячего тела переходит к холодному; газы стремятся занять наибольший объём.

2. Часть энергии переходит в теплоту, т. е. система из упорядоченного состояния переходит в состояние с беспорядочным тепловым движением частиц.

3. Самопроизвольные процессы можно использовать для получения полезной работы. По мере превращения система теряет способность производить работу. В конечном состоянии равновесия она имеет наименьший запас энергии.

4. Систему нельзя вернуть в исходное состояние, не производя каких-либо изменений в ней самой или в окружающей среде. Все самопроизвольные процессы термодинамически необратимы.

5. В самопроизвольном процессе начальное состояние является менее вероятным по сравнению с каждым последующим и наименее вероятным по сравнению с конечным.

Несамопроизвольные процессы протекают при затрате работы; при этом система удаляется от состояния равновесия (например, сжатие газа, электролиз).

Второй закон термодинамики – это постулат. Он имеет статистический характер и применим к системам из большого числа частиц.

Второй закон термодинамики имеет следующие формулировки:

1. Теплота не может переходить самопроизвольно от менее нагретого тела к более нагретому.

2. Невозможен процесс, единственным результатом которого является превращение теплоты в работу.

3. Вечный двигатель второго рода невозможен. Теплота, наиболее холодного из участвующих в процессе тел, не может служить источником работы.

Аналитическое выражение второго закона термодинамики и его обоснование с использованием цикла Карно. Суть выражения второго закона термодинамики – связь самопроизвольности процесса с ростом энтропии.Это выражение вытекает из рассмотрения вопроса о теоретической полноте превращения теплоты в работу в обратимом цикле Карно.

Цикл состоит из четырех процессов:

АВ – изотермическое расширение за счет теплоты Q_1, подведенной к газу при температуре Т₁;

ВС – адиабатическое расширение;

СД – изотермическое сжатие при температуре Т₂, в этом процессе газ теряет теплоту Q₂;

ДА – адиабатическое сжатие до исходного состояния.

Теплота, поглощаемая (или выделяемая) при изотермическом расширении (или сжатии) одного моль идеального газа, равна работе

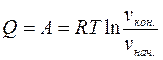. (4.1)

При адиабатическом расширении (или сжатии)

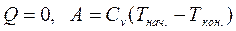. (4.2)

Применение этих уравнений к соответствующим процессам цикла приводит к выражению для термодинамического коэффициента полезного действия (к.п.д.): 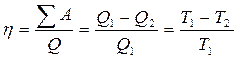. (4.3)

Уравнение (4.3) является математическим выражением второго закона термодинамики.

Так как T₁ ‹ T₂, то η ‹ 1.

Согласно теории Карно замена идеального газа любым другим веществом не приведет к изменению к.п.д. цикла Карно. Замена цикла Карно любым другим циклом приведет к меньшему к.п.д. (теорема Клазиуса-Карно). Таким образом, даже в случае идеальной тепловой машины превращение теплоты в работу не может быть полным.

Выражение второго закона термодинамики позволяет ввести понятие энтропии, с помощью которой сущность закона раскрывается в удобной и общей форме.

Изменим выражение (4.3):

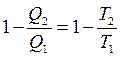на 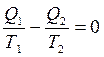. (4.4)

Отношение 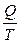называется приведенной теплотой. Уравнение (4.4) показывает, что алгебраическая сумма приведенных теплот по обратимому циклу Карно равна нулю.

Для бесконечно малого обратимого цикла Карно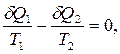

где 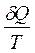- элементарная приведенная теплота.

Любой цикл может быть заменен совокупностью бесконечно малых циклов Карно: .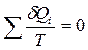

В пределе 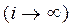эта сумма превратится в .

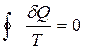В теории интегралов доказывается, что если интеграл по замкнутому контуру равен нулю, то подинтегральное выражение есть полный дифференциал некоторой функции от параметров, определяющих состояние системы.

,

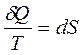где S – это энтропия, такая функция состояния системы, полный дифференциал которой в обратимом процессе равен отношению бесконечно малого количества теплоты к температуре.

Понятие «энтропия» введено Клаузиусом (1850). Это выражение является математическим выражением второго закона термодинамики для обратимых процессов.

Изменение энтропии в обратимом процессе равно изменению энтропии в необратимом процессе, т.е. 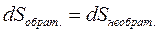. Сравним теплоты обратимого и необратимого процессов. Согласно первому закону термодинамики 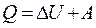. Внутренняя энергия U – это функция состояния системы, поэтому 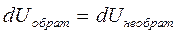. Максимальная работа совершается при обратимом процессе, поэтому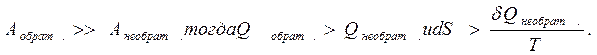

В общем случае для обратимого и необратимого процессов второй закон термодинамики имеет следующее математическое выражение:

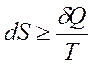. (4.5)

Здесь dS = const, а изменяется только правая часть уравнения, т.е. значение величины теплоты. Единицы измерения энтропии: [ S ] = Дж/моль·К.

Объединенное уравнение первого и второго закона термодинамики:

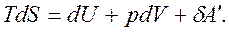(4.6)

Расчет изменения энтропии идеального газа.

Выразим изменение внутренней энергии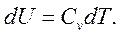

Разделив уравнение (4.6) на Т, определим изменение энтропии:

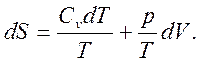(4.7)

Из уравнения идеального газа: 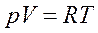следует, что 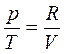. Тогда, после подстановки этого соотношения в (4.7):

(4.8)

Проинтегрируем выражение (4.8) при 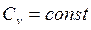и получим уравнение для расчета изменения энтропии идеального газа:

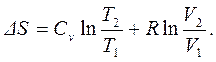(4.9)

Изотермический процесс, 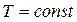: , (4.10)

так как 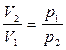, то 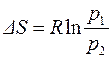. (4.11)

Изохорический процесс, 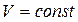: 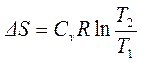. (4.12)

Изобарический процесс, 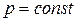: 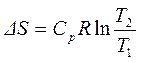. (4.13)

Адиабатический процесс, 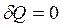: 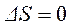. (4.14)

Постулат Планка имеет следующую формулировку: при абсолютном нуле энтропия правильно образованных кристаллов чистых веществ равна нулю. Постулат позволяет рассчитать абсолютное значение энтропии, если известны теплоты фазовых переходов, и если известны теплоёмкости вещества в различных агрегатных состояниях.

Рассмотрим вычисление изменения энтропии в различных процессах.

1. Изменение энтропии при фазовых переходах (T = const) определяется по формуле

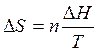, (4.15)

где ?H - теплота фазового перехода (кипение, испарение, возгонка, плавление); n – число моль вещества, переходящего из одной фазы в другую; n = g/M, где g – масса вещества, M – его молярная масса.

2. Изменение энтропии ?S при нагревании.

а) Пусть p = const, тогда , 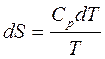. (4.16)

Если C_р = const, тогда ?S = C_р ln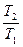, (4.17)

где Т₁ и Т₂ – температуры начала и окончания нагревания вещества.

Пусть C_р выражается в Дж/моль· К, тогда ?S = n C_р ln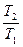, (4.18)

Пусть C_p выражается в Дж/г ·К, тогда ?S = g C_р ln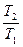. (4.19)

Если C_p зависит от температуры, т.е. C_р = f (T), тогда

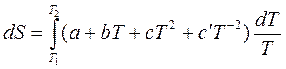. (4.20)

б) Пусть V = const, тогда 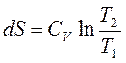. (4.21)

Для расчёта абсолютного значения энтропии S вещество нагревается от абсолютного нуля до данной температуры (p = const).

Для твёрдого тела при температуре T

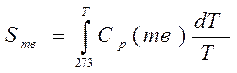. (4.22)

Для жидкости при температуре T

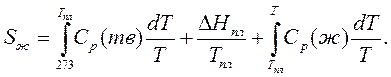(4.23)

Для газа при температуре T

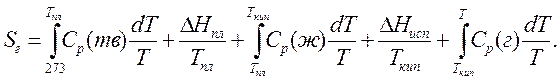(4.24)

Задача.

Найти изменение энтропии g кг вещества при нагревании (охлаждении) в интервале температур от Т₁ до Т₂, если известны температуры плавления и кипения, средние теплоемкости, теплоты плавления и испарения.