Термодинамическая вероятность

Состояние системы, определяемое термодинамическими параметрами (р, V, Т), называют макросостоянием, которое и наблюдается на опыте. В статистической физике число микросостояний, реализующих данное макросостояние системы, называют термодинамической вероятностью.

Поясним это на примере. Пусть в сосуде находятся шесть молекул газа. Мысленно разделим сосуд на три равные части.

Хаотически перемещаясь, молекулы создают определенные макрораспределения, некоторые из них показаны на рис. 43 а. Любое распределение, например, первое может быть осуществлено рядом микросостояний; некоторые из возможных микросостояний, дающих первое макросостояние, приведены на рис. 43 б.

В теоретической физике доказывается, что термодинамическая вероятность, т. е. количество возможных распределений N частиц по n состояниям (шесть частиц в трех частях сосуда), определяется формулой

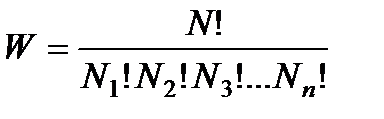, (147)

где N₁ – число частиц в первом состоянии (первой части сосуда); N₂ — число частиц во втором состоянии (второй части сосуда); N₃ — число частиц в третьем состоянии (третьей части сосуда) и т.д.

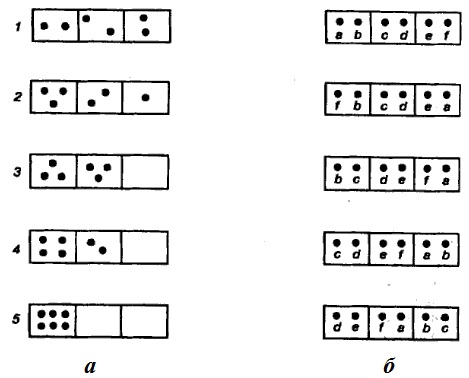
Рис. 43. К понятию термодинамической вероятности

Вычислим термодинамические вероятности макросостояний 1, 2, 3, 4, приведенных на рис. 43 а:

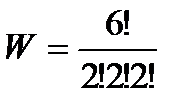= 90 – для состояния 1,

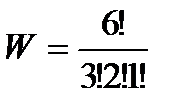= 60 – для состояния 2,

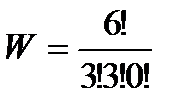= 20 – для состояния 3,

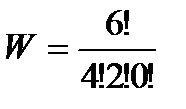= 15 – для состояния 4,

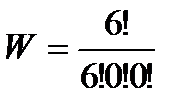= 90 – для состояния 5.

Наибольшая термодинамическая вероятность у равномерного распределения, оно может осуществляться наибольшим числом способов.

Связь энтропии с термодинамической вероятностью установил Больцман — энтропия пропорциональна логарифму термодинамической вероятности:

S = klnW, (148)

где k – постоянная Больцмана.

Формула (148) получила название формулы Больцмана.

Статистический смысл понятия энтропии состоит в том, что увеличение энтропии изолированной системы связано с переходом этой системы из менее вероятного состояния в более вероятное.

Одной из формулировок второго закона термодинамики, выявляющей статистический характер этого закона, является формулировка Больцмана: все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния.

Например, процесс диффузии в газах происходит потому, что равномерное распределение молекул по всему объему статистически будет более вероятным. Второй закон термодинамики является статистическим законом, выполняемым для замкнутых систем, состоящих из большого числа частиц. Второй закон неприменим для систем, состоящих из бесконечного числа частиц, так как для таких систем все состояния равновероятны.

Энтропия – аддитивная величина. Это означает, что энтропия системы равна сумме энтропий ее частей. Очевидно, уравнение Больцмана удовлетворяет этому свойству энтропии. Действительно, Вероятность сложного события, есть произведение вероятностей состояний:

W = W₁*W₂.

Отсюда

lnW = lnW₁ + lnW₂.

При термодинамическом определении энтропии мы встретились с трудностью распространения этого понятия на случай термодинамически неравновесных состояний. Формула Больцмана (148) дает принципиальный способ преодоления указанной трудности. Надо смотреть на нее как на определение энтропии. Правда, для того чтобы это определение получило конкретное содержание, надо дополнить его способами вычисления вероятностей состояний во всех требуемых случаях. Но и без этого видно, что при таком понимании энтропии закон ее возрастания коренным образом меняет свой характер. Он утрачивает свою абсолютность и превращается в статистический закон. Энтропия замкнутой системы может не только возрастать, но и убывать.

И она действительно будет убывать, если только подождать достаточно долго. Однако процесс убывания снова сменится в дальнейшем процессом возрастания. Что же остается в таком случае от второго начала термодинамики? В чем состоит его физическое содержание? А в том, что за каким-либо заданным состоянием системы будут следовать состояния еще более вероятные, если и не с необходимостью, то в подавляющем большинстве случаев. Если система большая, а исходное состояние ее не очень близко к состоянию равновесия, то переходы системы в менее вероятные состояния будут настолько маловероятны, что на практике они совершенно не имеют никакого значении. Тогда закон возрастания энтропии оправдывается практически с абсолютной достоверностью.

Рассчитаем вероятность таких процессов. Пусть в сосуде находится всего одна молекула. Тогда, если нет внешних силовых полей, молекула с равной вероятностью может попасть либо в часть 1, либо в часть 2. Вероятности попадании ее в эти одинаковые части Р₁ = Р₂ = ¹/.₂. Введем в сосуд вторую молекулу. Так как молекулы идеального газа не взаимодействуют между собой, то их попадания в ту или иную часть сосуда будут независимыми событиями. Вероятность того, что обе они окажутся в части 1, найдется по теореме умножения вероятностей и будет равна P₁ = ¹/₂ ¹/₂ = ¹/₄.

Если в сосуде N молекул, то, рассуждая аналогично, найдем, что вероятность их попадания в часть 1 будет P₁ = (¹/₂) ^N. При N = 10 получаем Р₁ = (¹/₂)¹⁰ = ¹/₁₀₂₄ ≈ 0,001. Если в течение длительного (в пределе бесконечно длительного) времени фотографировать распределение молекул в сосуде через равные промежутки времени, то на каждые 1000 кадров в среднем придется приблизительно один кадр, на котором будут зафиксированы все 10 молекул только в части сосуда 1. То же можно сказать и о части 2.

По теореме сложения вероятностей получится в среднем 2 кадра на каждую тысячу с молекулами, сосредоточенными либо в части 1, либо в части 2 (безразлично какой). Все это не только принципиально возможно, но и фактически доступно наблюдению. Однако при N = 100 мы получаем P₁ = (1/2)¹⁰⁰ ≈ 10^-30, и практически нет никаких шансов наблюдать соответствующую флуктуацию. При N равном числу Авогадро для соответствующей вероятности получается настолько чудовищно малая величина, что с такого рода вероятностями и соответствующими им событиями можно совершенно не считаться.

Рассмотрим еще раз рис. 1а. Энтропия системы максимальна для 1-го состояния. Это состояние является наиболее хаотическим, или наиболее разупорядоченным. В этом состоянии система абсолютно однородна. Состояния 2, 3, 4, 5 характерны тем, что система становится неоднородной, в расположении частиц появляется упорядоченность. При движении от 1-го состояния до 5-го в расположении частиц все больше порядка (увеличивается упорядоченность, или увеличивается неоднородность системы), и при этом понижается энтропия. Наименьшей энтропией обладает вариант 5, когда все частицы расположены в одном месте. В этом случае система максимально неоднородна (или максимально упорядочена).