При квантовомеханическом рассмотрении для полного описания состояния системы в самом общем виде используется вектор состояния 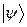 (в обозначениях Дирака). При этом, если имеется полный набор собственных состояний некоторой динамической переменной
(в обозначениях Дирака). При этом, если имеется полный набор собственных состояний некоторой динамической переменной 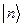 , образующих ортонормированный базис (для определенности будем говорить об энергии), то согласно принципа суперпозиции,
, образующих ортонормированный базис (для определенности будем говорить об энергии), то согласно принципа суперпозиции, 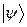 можно разложить по этому базису:
можно разложить по этому базису:
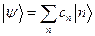 (1)
(1)
Коэффициенты 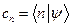 в этом соотношении можно определить как «проекции», соответственно чему введем оператор проектирования на состояние
в этом соотношении можно определить как «проекции», соответственно чему введем оператор проектирования на состояние 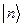
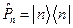 , (2)
, (2)
так что
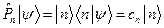 .
.
Суммируя по 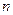 , получаем, используя (1):
, получаем, используя (1):
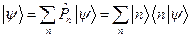 ,
,
откуда следует условие нормировки: 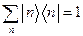 .
.
Если система находится в определенном состоянии 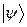 , то квантовомеханическое среднее величины
, то квантовомеханическое среднее величины 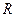 в этом состоянии определяется как:
в этом состоянии определяется как:
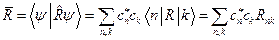 .
.
С другой стороны, такое же выражение для среднего можно получить, вычисляя его как след оператора 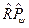 в исходном базисе:
в исходном базисе:
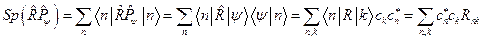
Заметим, что это выражение инвариантно относительно выбора базиса.
Если же состояние системы 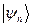 (
(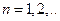 ) точно не определено, а может реализоваться с определенной вероятностью
) точно не определено, а может реализоваться с определенной вероятностью 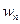 , что имеет место при ее взаимодействии с окружающей ее системой (термостатом), то
, что имеет место при ее взаимодействии с окружающей ее системой (термостатом), то 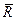 естественно определить как среднее по всевозможным реализациям
естественно определить как среднее по всевозможным реализациям 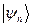 с соответствующими вероятностями (
с соответствующими вероятностями (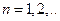 ):
):
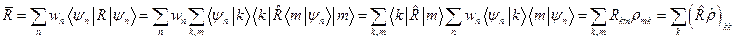
где 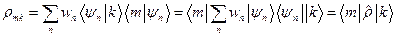 - элемент матрицы плотности, построенный на исходной системе собственных функций, который также можно назвать матричным элементом статистического оператора
- элемент матрицы плотности, построенный на исходной системе собственных функций, который также можно назвать матричным элементом статистического оператора
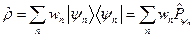 .
.
Полученное выражение для среднего можно записать в виде, не зависящем от выбора базиса:
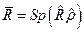 .
.
Если равны нулю все 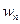 , кроме одного, то состояние системы определено точно, и о нем говорят как о чистом. В противном случае система обнаруживает себя сразу в нескольких состояниях, и о таком состоянии говорят как о смешанном. Отметим, что в чистом состоянии, как следует из определения
, кроме одного, то состояние системы определено точно, и о нем говорят как о чистом. В противном случае система обнаруживает себя сразу в нескольких состояниях, и о таком состоянии говорят как о смешанном. Отметим, что в чистом состоянии, как следует из определения 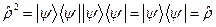 .
.
Эволюционное уравнение для матрицы плотности получим, используя представление:
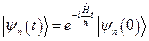
Тогда
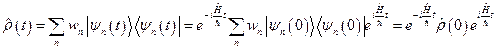
Отсюда можно видеть, что 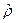 подчиняется уравнению
подчиняется уравнению
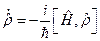 .
.
Для системы, находящейся в состоянии термодинамического равновесия, распределение 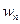 является гиббсовским:
является гиббсовским:
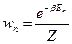 ,
, 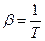 .
.
В координатном представлении матрица плотности является функцией двух переменных. Если 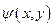 - волновая функция, соответствующая чистому состоянию системы с термостатом, то матрица плотности в координатном представлении получается интегрированием по координатам термостата:
- волновая функция, соответствующая чистому состоянию системы с термостатом, то матрица плотности в координатном представлении получается интегрированием по координатам термостата:
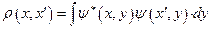
Отсюда видно, что плотность вероятности обнаружить частицу в заданной точке определяется диагональным матричным элементом 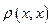 после интегрирования по переменным термостата.
после интегрирования по переменным термостата.
Представим ее в виде разложения по с. ф. гамильтониана, используя явный вид 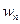 :
:
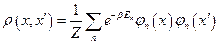 .
.
Т. к. 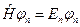 , то соответствующий статистический оператор представим в виде:
, то соответствующий статистический оператор представим в виде:
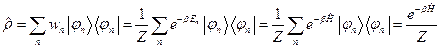
в силу условия нормировки. Тогда статистический интеграл и среднюю энергию можно представить в инвариантной форме:
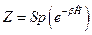 ,
,
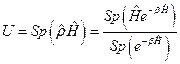 ,
,
Помимо 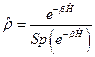 удобно ввести также «ненормированный» статистический оператор
удобно ввести также «ненормированный» статистический оператор 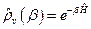 , для которого, справедливо уравнение:
, для которого, справедливо уравнение:
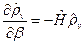 ,
,
с «начальным» условием (при 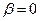 )
) 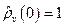 (оператор
(оператор 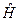 действует на переменную
действует на переменную 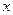 ). Для того, чтобы убедиться в этом, достаточно записать матрицу плотности в энергетическом представлении в виде:
). Для того, чтобы убедиться в этом, достаточно записать матрицу плотности в энергетическом представлении в виде:
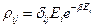
и продифференцировать полученное равенство по 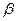 .
.
Тогда для матричных элементов этого оператора в координатном представлении (т. е. для координатной матрицы плотности), получаем:
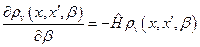
с начальным условием 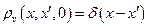 .
.
 2015-10-13
2015-10-13 2000
2000








