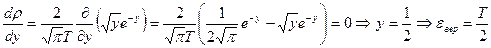
35. Найти вероятность того, что две частицы имеют абсолютные значения скорости относительного движения 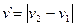 в интервале от
в интервале от 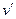 до
до 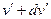 . Найти также
. Найти также 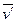 .
.
Решение: Ввиду независимости движения частиц функция распределения распадается на произведение функций распределения каждой из частиц:
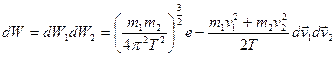 , где
, где 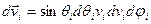 .
.
Перейдем от 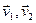 к новым переменным – относительной скорости
к новым переменным – относительной скорости 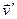 и скорости центра масс
и скорости центра масс 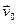 :
:
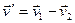 ,
, 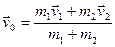 , следовательно
, следовательно 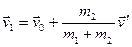 ,
, 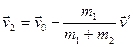 (якобиан перехода равен единице) и
(якобиан перехода равен единице) и 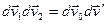 .
.
Далее нетрудно показать, что
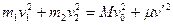 ,
,
где 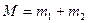 , а
, а 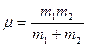 - приведенная масса
- приведенная масса 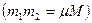 .
.
Следовательно
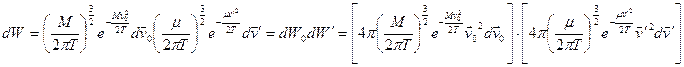 Функция распределения по относительной скорости
Функция распределения по относительной скорости 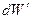 получается отсюда интегрированием по
получается отсюда интегрированием по 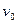 (обе функции распределения автоматически нормированы).
(обе функции распределения автоматически нормированы).
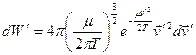 .
.
Среднее значение относительной скорости:
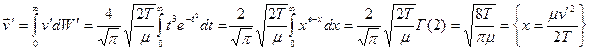 =
=
{если частицы одного сорта, то 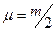 } =
} = 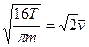 .
.
36. 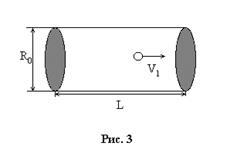 Найти число соударений в единицу времени молекулы радиуса
Найти число соударений в единицу времени молекулы радиуса 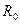 и среднюю длину свободного пробега. Концентрация молекул
и среднюю длину свободного пробега. Концентрация молекул 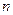 .
.
Решение:
Если считать, что газ однородный, и зафиксировать все частицы кроме одной, то она будет двигаться по цилиндрической трубе со скоростью 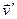 , пока не встретит «неподвижную» частицу. Тогда из элементарной пропорции находим:
, пока не встретит «неподвижную» частицу. Тогда из элементарной пропорции находим: 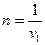 , (т. к. в цилиндре находится только одна частица). Очевидно:
, (т. к. в цилиндре находится только одна частица). Очевидно:
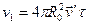 ,
,
где t - среднее время между столкновениями. Число столкновений в единицу времени:
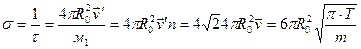 .
.
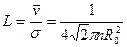
37. Запирающий потенциал, создающий электронным облаком вблизи поверхности 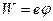 . Определить плотность тока термоэлектронной эмиссии.
. Определить плотность тока термоэлектронной эмиссии.
Решение:
Вклад в термоэлектронную эмиссию дают лишь те электроны, скорость которых подчиняется условию (ось 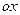 перпендикулярна поверхности).
перпендикулярна поверхности).
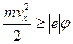 .
.
Вклад в термоэлектронный ток электронов, движущихся в интервале скоростей 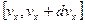 , определяется распределением Максвелла:
, определяется распределением Максвелла:
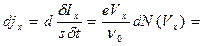 {
{ 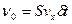 } =
} =
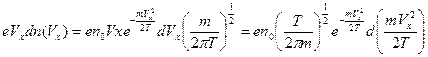 .
.
Следовательно
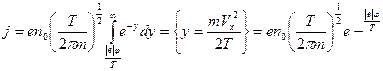
38. Найти центр масс столбом идеального газа в однородном поле тяжести, считая температуру неизменной.
Решение: Если проинтегрировать исходное распределение по всем скоростям, то получим распределение Больцмана:
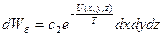 ,
,
определяющее вероятность координаты одной частицы (по координатам и импульсам остальных частиц мы также проинтегрировали). Остается еще проинтегрировать по 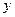 и
и 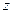 и все интегралы включить в
и все интегралы включить в 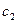 . тогда, в случае однородного поля (
. тогда, в случае однородного поля (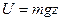 )
)
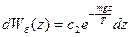 ,
, 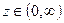 .
.
Находим из условия нормировки: 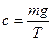 .
.
Положение центра масс находим по общей формуле:
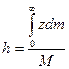 , но
, но 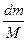 - есть вероятность координаты (
- есть вероятность координаты (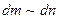 ). Поэтому:
). Поэтому:
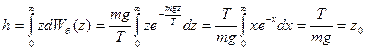 .
.
(здесь 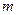 – масса одной молекулы)
– масса одной молекулы)
NB 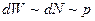 , следовательно, в приближении изотермичности атмосферы получаем барометрическую формулу
, следовательно, в приближении изотермичности атмосферы получаем барометрическую формулу 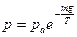 .
.
39. Смесь 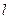 идеальных газов, состоящих из одинакового количества частиц с различными массами атомов, заключена в цилиндр высоты
идеальных газов, состоящих из одинакового количества частиц с различными массами атомов, заключена в цилиндр высоты 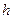 и помещена в поле тяжести Земли. Определить центр масс системы.
и помещена в поле тяжести Земли. Определить центр масс системы.
Решение: С учетом результата предыдущей задачи перепишем распределение в виде:
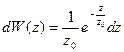 ,
, 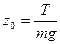 .
.
Тогда центр тяжести одного сорта частиц:
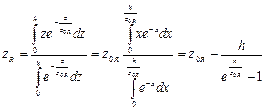 .
.
Общий центр тяжести:
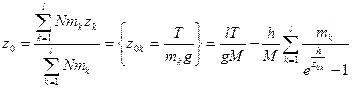
40. Вывести закон Дальтона для смеси N идеальных газов 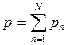 , где
, где 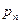 – парциальное давление.
– парциальное давление.
Решение: Гамильтониан смеси: 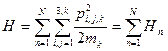 .
.
Это означает, что зависимость 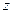 от объема имеет следующий вид:
от объема имеет следующий вид:
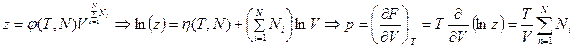 ,
,
но 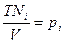 - парциальное давление и, следовательно
- парциальное давление и, следовательно 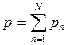
41.  В тонкостенном сосуде, содержащем идеальный газ с концентрацией
В тонкостенном сосуде, содержащем идеальный газ с концентрацией 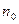 и средней скорости молекул
и средней скорости молекул 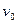 , проделано небольшое круглое отверстие сечением
, проделано небольшое круглое отверстие сечением 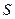 . Определить число молекул, попадающих в единицу времени на круглый диск радиуса
. Определить число молекул, попадающих в единицу времени на круглый диск радиуса 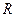 , находящийся на расстоянии
, находящийся на расстоянии 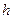 от отверстия.
от отверстия.
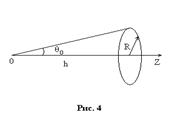
Решение: Число частиц, вылетающих в единицу времени из отверстия и движущихся поду углами в интервале 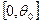 (и, естественно попадающих на диск, см. рис. 4) к оси
(и, естественно попадающих на диск, см. рис. 4) к оси 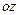 :
:
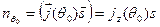 ,
,
где 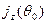 -
- 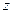 –компонента плотности потока таких молекул. Считая, что скорости молекул распределены по Максвеллу, получаем:
–компонента плотности потока таких молекул. Считая, что скорости молекул распределены по Максвеллу, получаем:
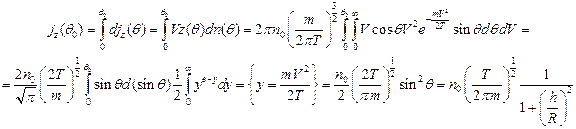
С учетом того, что средняя скорость молекул: 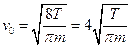
получаем 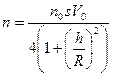 .
.
NB При 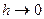 получаем скорость истечения газа из отверстия
получаем скорость истечения газа из отверстия 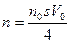 -.
-.
41. Определить среднюю скорость молекул, выходящих из отверстия.
Решение: Воспользуемся распределением Максвелла. При этом нас будет интересовать только 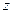 – проекция скорости. Число частиц, имеющих скорость в интервале
– проекция скорости. Число частиц, имеющих скорость в интервале 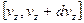 :
:
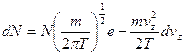 . Следовательно, средняя скорость
. Следовательно, средняя скорость 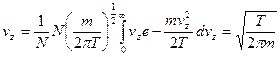 .
.
 2015-10-13
2015-10-13 2140
2140








