- Для свободной частицы
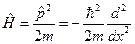 и мы получаем уравнение диффузии. Решение, удовлетворяющее начальному условию имеет вид:
и мы получаем уравнение диффузии. Решение, удовлетворяющее начальному условию имеет вид:
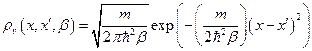 .
.
Для нахождения статистической суммы достаточно взять след от обеих частей полученного равенства:
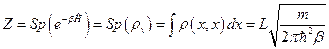 ,
,
где 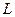 - линейный размер системы.
- линейный размер системы.
Явный вид 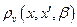 для свободной частицы в термостате можно получить и по-другому, если в исходном выражении:
для свободной частицы в термостате можно получить и по-другому, если в исходном выражении:
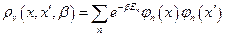
Перейти от суммирования к интегрированию с помощью замен:
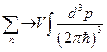 ,
, 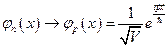 .
.
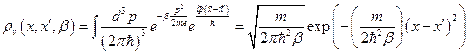 .
.
- Осциллятор.
Гамильтониан имеет вид 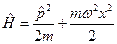 , поэтому соответствующее уравнение
, поэтому соответствующее уравнение
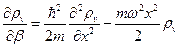 .
.
Введем безразмерную координату и обратную температуру:
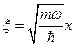 ,
, 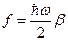 .
.
В новых переменных уравнение примет вид:
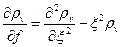
с начальным условием 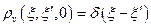 . Будем искать его решение в виде гауссовского с некоторыми коэффициентами, подлежащими определению:
. Будем искать его решение в виде гауссовского с некоторыми коэффициентами, подлежащими определению:
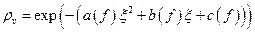 .
.
Подставляя в уравнение, выполняя дифференцирование и приравнивая друг другу коэффициенты при различных степенях 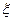 , получаем систему для определения
, получаем систему для определения 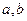 и
и 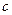 (штрих означает производную по
(штрих означает производную по 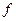 ):
):
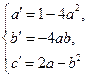
Откуда 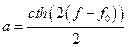 , причем в силу начального условия для гауссовского распределения
, причем в силу начального условия для гауссовского распределения 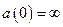 , следовательно,
, следовательно, 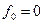 и
и
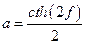
Интегрируя оставшиеся уравнения, получаем:
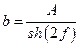 ,
, 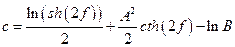 .
.
где 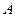 и
и 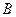 - константы интегрирования. Таким образом:
- константы интегрирования. Таким образом:
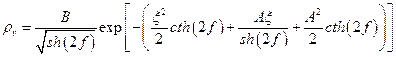 .
.
Для определения 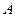 и
и 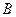 заметим, что при высоких температурах (
заметим, что при высоких температурах (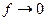 ) кинетическая энергия осциллятора велика, и поэтому его матрица плотности должна совпадать с матрицей плотности для свободной частицы:
) кинетическая энергия осциллятора велика, и поэтому его матрица плотности должна совпадать с матрицей плотности для свободной частицы:
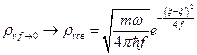 .
.
С другой стороны очевидно, что
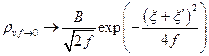
Сравнивая два последних выражения, находим, что:
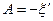 ,
, 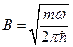 .
.
Таким образом
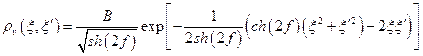
При 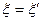 получаем плотность вероятности обнаружить осциллятор в заданной точке пространства:
получаем плотность вероятности обнаружить осциллятор в заданной точке пространства:
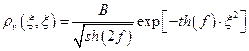 .
.
С помощью найденной функции находим
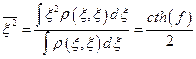 ,
,
Следовательно, среднее значение потенциальной энергии
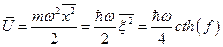 .
.
Среднее значение полной энергии, вычисленное с помощью статистической суммы (см. зад. 19)
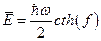 ,
,
и сразу можно найти среднюю кинетическую энергию:
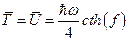
Статистическая сумма для осциллятора:
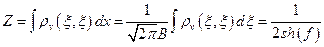
что совпадает с результатом задачи (19).
Свободная энергия:
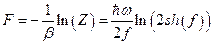
 2015-10-13
2015-10-13 535
535








