Средняя энергия системы (твердое тело, состоящее из 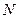 атомов)
атомов) 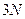 осцилляторов с одинаковой частотой
осцилляторов с одинаковой частотой 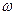 была найдена ранее:
была найдена ранее:
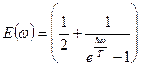
однако если существует спектр колебаний, т.е. число колебаний на интервал энергий 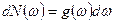 , то
, то
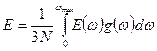 .
.
Нашей целью будет найти 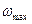 и
и 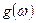 .
.
Будем использовать следующую модель: Куб стороной 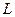 , в котором происходят колебания, которые будем представлять себе как колебания атомов в поле упругих волн. Эти волны могут быть двух видов: продольные и поперечные, которым соответствуют разные фазовые скорости
, в котором происходят колебания, которые будем представлять себе как колебания атомов в поле упругих волн. Эти волны могут быть двух видов: продольные и поперечные, которым соответствуют разные фазовые скорости 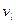 и
и 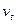 и уравнения:
и уравнения:
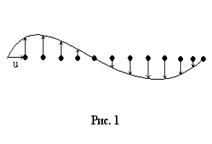
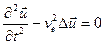 и
и 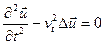 ,
,
где 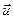 - вектор смещения (в продольной волне
- вектор смещения (в продольной волне 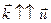 , в поперечной
, в поперечной 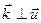 ). Граничные условия для
). Граничные условия для 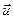 выберем в виде
выберем в виде 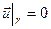 . Рассмотрим, например, –волну. Ищем решение в виде стоячей волны:
. Рассмотрим, например, –волну. Ищем решение в виде стоячей волны:
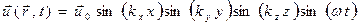 .
.
Подставляя в уравнение, находим, используя граничные условия:
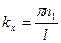 ,
, 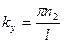 ,
, 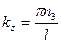 ,
,
где 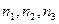 – целые числа.
– целые числа.
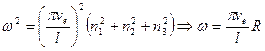 ,
,
где 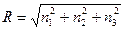 - некоторый радиус
- некоторый радиус
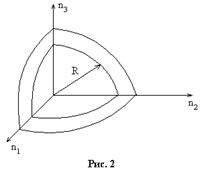 Таким образом, каждое колебание характеризуется набором трех целых чисел
Таким образом, каждое колебание характеризуется набором трех целых чисел 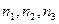 , которым в пространстве чисел
, которым в пространстве чисел 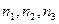 соответствует точка. Кроме того, колебания
соответствует точка. Кроме того, колебания 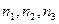 и
и 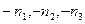 зависимы, следовательно, можно рассматривать только целые положительные
зависимы, следовательно, можно рассматривать только целые положительные 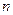 . Так как
. Так как 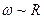 , то число колебаний в интервале частот
, то число колебаний в интервале частот 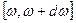 равно объему сферического слоя (т.к. объем одной ячейки, соответствует, одному колебанию равен единице):
равно объему сферического слоя (т.к. объем одной ячейки, соответствует, одному колебанию равен единице):
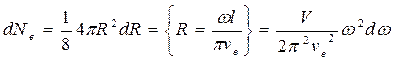 , (V = l3 – объем кристалла)
, (V = l3 – объем кристалла)
Полное число колебаний:
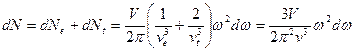 , где
, где 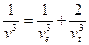 .
.
(так как поперечных колебаний два). Таким образом:
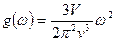
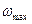 – найдем из условия нормировки:
– найдем из условия нормировки:
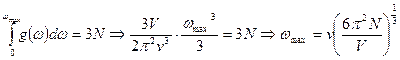
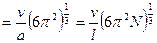 ,
,
где 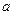 – постоянная решетки
– постоянная решетки 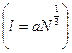 .
.
Подставляя в выражение для энергии, получаем:
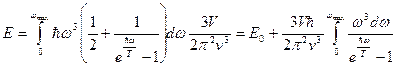
Если ввести температуру Дебая
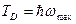 ,
,
то выражение для энергии можно переписать в виде:
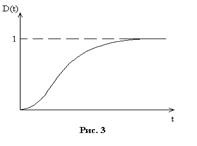
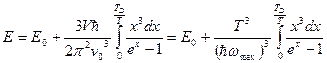 .
.
Введем функцию Дебая
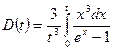 (рис. 3).
(рис. 3).
Тогда выражение для энергии перепишется в окончательном виде:
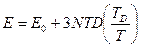 .
.
Предельные случаи:
-
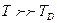 , следовательно, верхний предел в интеграле
, следовательно, верхний предел в интеграле 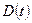 – мал. Тогда подынтегральную функцию можно разложить в ряд:
– мал. Тогда подынтегральную функцию можно разложить в ряд:
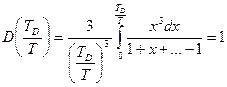 .
.
Тогда 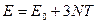 и, следовательно
и, следовательно 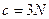 – классический закон Дюлонга-Пти.
– классический закон Дюлонга-Пти.
-
 (низкотемпературный предел). В этом случае верхний предел интегрирования можно заменить на
(низкотемпературный предел). В этом случае верхний предел интегрирования можно заменить на 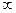 .
.
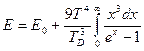
интеграл равен 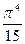 (см. ниже). Тогда:
(см. ниже). Тогда:
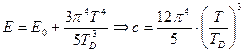 .
.
 2015-10-13
2015-10-13 537
537








