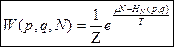 ,
,
где 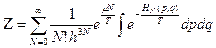 ,
, 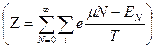 ,
,
большой статистический интеграл (статистическая сумма).
Большое каноническое распределение описывает распределение вероятностей не только координат и импульсов, но и числа частиц. Оно справедливо, в частности, для химических реакций и фазовых превращений. Обозначим, по аналогии со свободной энергией:
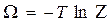 .
.
Очевидно, что 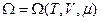 , следовательно:
, следовательно:
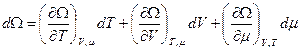 .
.
Непосредственным дифференцированием получаем:
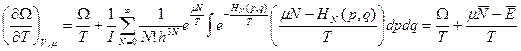
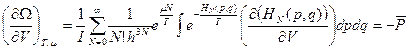
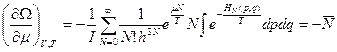
(средние получены по общей формуле при помощи плотности распределения 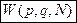 ).
).
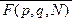
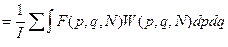 ).
).
Следовательно:
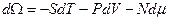 ,
,
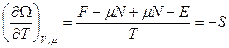 ,
, 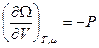 ,
, 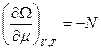 .
.
Этим соотношением можно удовлетворить положив:
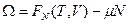 ,
,
где 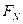 – свободная энергия
– свободная энергия 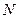 частиц.
частиц.
Так как 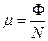 (см. термодинамику с переменным числом частиц), то
(см. термодинамику с переменным числом частиц), то
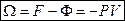
 2015-10-13
2015-10-13 830
830








