Воспользуемся БКР, записав его в виде:
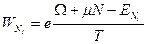 - вероятность того, что система содержит
- вероятность того, что система содержит 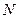 частиц и находится в
частиц и находится в 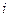 –м квантовом состоянии.
–м квантовом состоянии.
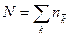 ,
, 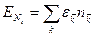
Вектор 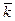 - обозначает квантовое состояние,
- обозначает квантовое состояние, 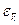 - его энергия,
- его энергия, 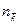 - число частиц в этом состоянии.
- число частиц в этом состоянии.
Подставляя эти выражения, находим:
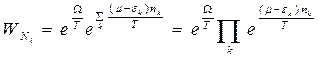 .
.
Каждый из множителей представляет собой вероятность того, что в данном кантовом состоянии находится 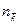 частиц.
частиц.
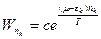
Из условия нормировки находим 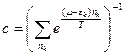 .
.
Среднее число частиц в 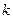 –м квантовом состоянии:
–м квантовом состоянии:
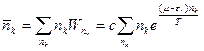 ={с учетом
={с учетом 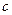 }=
}= 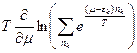 .
.
Для фермионов: 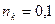 , следовательно
, следовательно 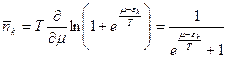 .
.
Для бозонов: 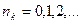
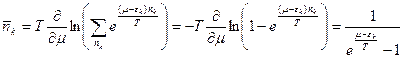 .
.
Итак, квантовые статистики имеют вид:
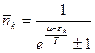 (Знак плюс соответствует фермионам, минус - бозонам).
(Знак плюс соответствует фермионам, минус - бозонам).
Должно выполняется очевидное равенство:
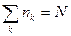
Переходя к непрерывному распределению состояний, получаем
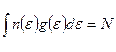
где 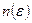 – число частиц в одном квантовом состоянии, соответствующем энергии
– число частиц в одном квантовом состоянии, соответствующем энергии 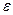 ,
, 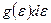 - число состояний в интервале энергий
- число состояний в интервале энергий 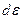 . Найдем его. Из квантовой механики известно, что энергия свободной частицы в кубе со стороной,
. Найдем его. Из квантовой механики известно, что энергия свободной частицы в кубе со стороной, 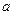 равна
равна
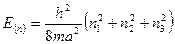 ,
, 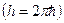 .
.
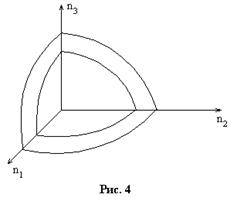 (решая уравнение Шредингера
(решая уравнение Шредингера 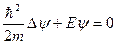 с условием
с условием 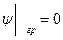
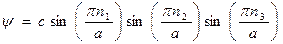 ),
), 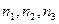 - целые положительные числа.
- целые положительные числа.
Рассмотрим пространство этих чисел. Каждое состояние описывается точкой с численными координатами, причем состояния 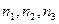 и, например,
и, например, 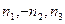 зависимы. Поэтому имеет смысл рассматривать только положительные
зависимы. Поэтому имеет смысл рассматривать только положительные 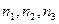 . Обозначим
. Обозначим 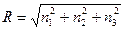 - радиус. Очевидно
- радиус. Очевидно
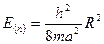
Число состояний с энергиями в интервале 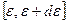 равно
равно 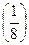 -объема шарового слоя (т.к. объем одной ячейки равен единице):
-объема шарового слоя (т.к. объем одной ячейки равен единице):
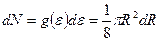 .
.
Однако полное число состояний будет еще в 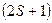 раз больше (что соответствует
раз больше (что соответствует 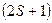 проекции спина):
проекции спина):
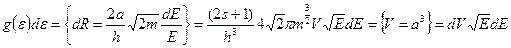 .
.
NB Для двумерного случая 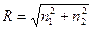
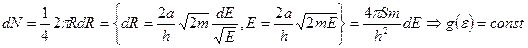
Для одномерного случая 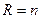 :
:
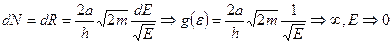
Возвращаясь к трехмерному случаю, пишем:
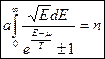 , (*)
, (*)
где – концентрация.
Задачи
42. Получить статистики Бозе и Ферми из канонического распределения.
Решение: Рассмотрим состояние, описываемое полным набором квантовых чисел со значением энергии 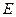 . Если состояние заселено
. Если состояние заселено 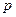 невзаимодействующими частицами, то его энергия
невзаимодействующими частицами, то его энергия 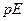 . Тогда
. Тогда
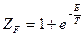
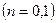 ,
,
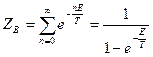
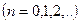 .
.
Согласно формуле
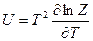 .
.
Подставляя, находим:
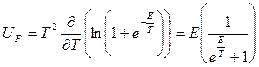
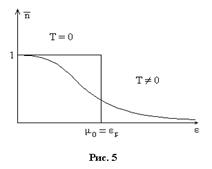
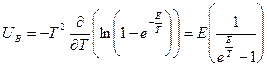
График распределения при различных 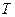 имеет вид: (Ферми), представленный на рис.5.
имеет вид: (Ферми), представленный на рис.5. 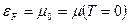 - энергия Ферми, которую можно получить следующим образом: При
- энергия Ферми, которую можно получить следующим образом: При 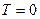 все
все 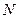 электронов находятся внутри сферы
электронов находятся внутри сферы 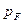 в пространстве импульсов (наинизшее энергетическое состояние). Так как каждым двум состояниям (спины вверх и вниз) соответствует в фазовом пространстве ячейка размером
в пространстве импульсов (наинизшее энергетическое состояние). Так как каждым двум состояниям (спины вверх и вниз) соответствует в фазовом пространстве ячейка размером 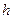 , то
, то
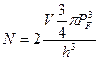 .
.
Т.к. 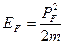 , то
, то
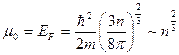
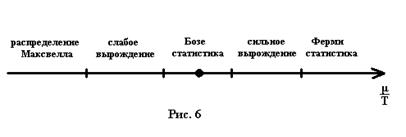
NB Величина 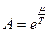 называется активностью (рис. 6)
называется активностью (рис. 6)
1) Если 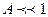 (
(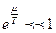 ) то распределение переходит в распределение Максвелла (Говорят, что газ в этом случае невырожден, чему соответствует
) то распределение переходит в распределение Максвелла (Говорят, что газ в этом случае невырожден, чему соответствует 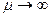 ).
).
2) Если 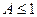 (
(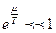 ), то газ называется слабовырожденным (
), то газ называется слабовырожденным (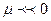 ).
).
3) Если 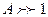 (
(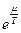 >> 1), то газ будет сильновырожденным (
>> 1), то газ будет сильновырожденным (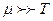 )
)
43. Найти температурную зависимость химического потенциала при слабом вырождении
Решение: Перепишем (*) в виде (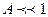 )
)
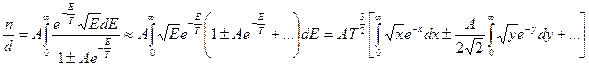 =
=
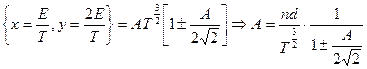 .
.
В нулевом приближении 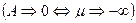 получаем распределение Максвелла:
получаем распределение Максвелла:
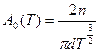 .
.
Газ становится вырожденным, когда 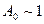 . Отсюда
. Отсюда 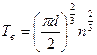 .
.
Если 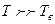 то газ подчиняется классической статистике, если
то газ подчиняется классической статистике, если 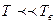 – квантовой.
– квантовой.
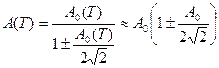 .
.
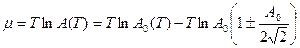 .
.
44. 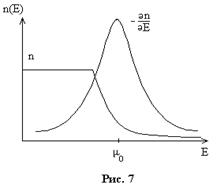 Найти температурную зависимость химического потенциала сильно вырожденного газа.
Найти температурную зависимость химического потенциала сильно вырожденного газа.
Решение: Сильновырожденным может быть только Ферми – газ, т.к. для Бозе – газов 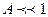 , а в нашем случае
, а в нашем случае 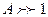 (
(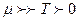 )
)
При 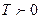
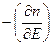 будет иметь резкий максимум при
будет иметь резкий максимум при 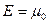 . При
. При 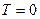
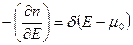 .
.
Преобразуем интеграл выражения (*):
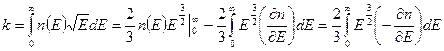 ,
,
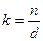 . При
. При 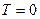 получаем
получаем 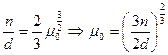 .
.
Т.к. 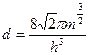 (для
(для 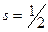 ), то
), то 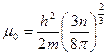 (что совпадает с ранее полученными выражениями).
(что совпадает с ранее полученными выражениями).
Итак
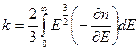 .
.
Введем новую переменную 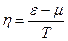 , тогда:
, тогда:
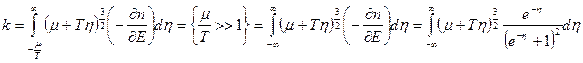 .
.
Рассмотрим этот интеграл отдельно, функция 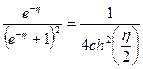 быстро спадает и
быстро спадает и 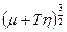 можно разложить в ряд вблизи
можно разложить в ряд вблизи 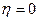 :
:
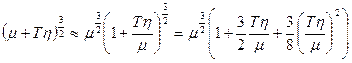 .
.
Т.к. функция 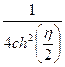 - четная, то интегрирование ее со вторым слагаемым, дает нуль.
- четная, то интегрирование ее со вторым слагаемым, дает нуль.
Остается
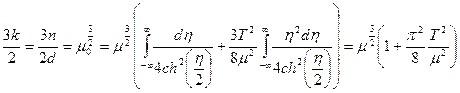
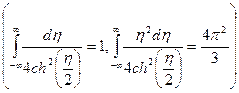
В скобке можно положить 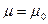 . Следовательно
. Следовательно
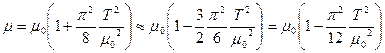 .
.
45. Рассмотреть Бозе – конденсацию.
Решение: Для трехмерного Бозе – газа (см. ниже) справедливо соотношение:
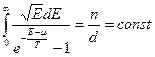 .
.
(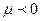 , в противном случае для
, в противном случае для 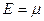
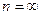 ) (при уменьшении
) (при уменьшении 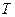
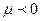 должно уменьшаться по абсолютной величине). Таким образом, имеется два параметра
должно уменьшаться по абсолютной величине). Таким образом, имеется два параметра 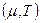 , подбирая которые можно оставлять интеграл неизменным. При некоторой температуре
, подбирая которые можно оставлять интеграл неизменным. При некоторой температуре 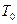
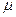 обращается в нуль (
обращается в нуль (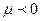 ), и изменяя далее
), и изменяя далее 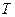 мы изменяем
мы изменяем 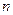 . На самом деле никакого противоречия здесь нет, т.к.
. На самом деле никакого противоречия здесь нет, т.к. 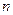 – концентрация частиц с
– концентрация частиц с 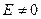 (множитель
(множитель 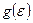 не учитывает частицы на самом нижнем энергетическом уровне). Следовательно, при понижении
не учитывает частицы на самом нижнем энергетическом уровне). Следовательно, при понижении 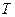 частицы начинают скапливаться на уровне
частицы начинают скапливаться на уровне 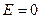 . Определим температуру, при которой
. Определим температуру, при которой 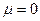 :
:
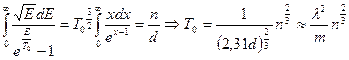
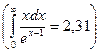 .
.
При 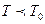
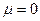 и число частиц с
и число частиц с 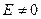 :
:
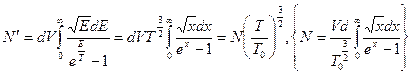
Число частиц на нижнем уровне
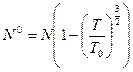 .
.
46. Найти внутреннюю энергию и давление Ферми и Бозе - газов.
Решение: Найдем большую статистическую сумму для Ферми или бозе - газа, воспользуемся ее мультипликативностью для различных квантовых состояний 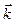 :
:
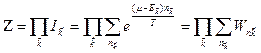 ,
,
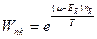
(см. Ферми и Бозе - газы). Взяв эту сумму для Ферми и Бозе газа (это делалось ранее), находим 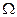
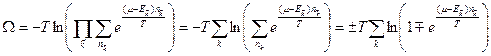
где верхние знаки соответствуют бозонам, а нижние – фермионам. Перейдем от суммирования по состояниям к интегрированию по 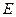 :
:
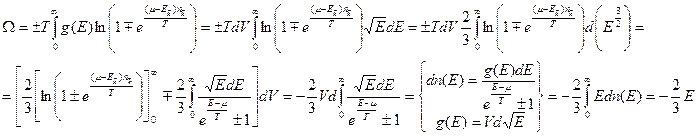
Т.к. 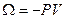 , то
, то
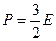 .
.
47. Доказать, что двумерный и одномерный Бозе-газы не обладают свойством конденсации.
Решение:
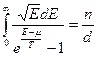
для трехмерных газов в одно- и двумерном случае будут иметь вид (ранее были найдены  и
и 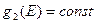 ).
).
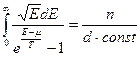 ,
,
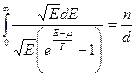 .
.
Очевидно, что одномерный Бозе - газ вообще не может существовать, т.к.  и интеграл расходится. Что же касается двумерного газа, то ввиду того, что
и интеграл расходится. Что же касается двумерного газа, то ввиду того, что 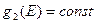 , интеграл учитывает также частицы с
, интеграл учитывает также частицы с 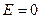 и это состояние невозможно отделить от остальных. Кроме того, при конечных температурах теперь
и это состояние невозможно отделить от остальных. Кроме того, при конечных температурах теперь 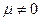 т.к. ввиду постоянства интеграла, он должен быть неизменным. Однако очевидно, что он зависит от
т.к. ввиду постоянства интеграла, он должен быть неизменным. Однако очевидно, что он зависит от 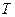 и, следовательно, должен быть еще один изменяющийся параметр
и, следовательно, должен быть еще один изменяющийся параметр 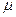 .
.
48. Найти энергию Бозе-газа в области конденсации (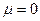 ).
).
Решение: В задаче 5 было указано на то, что для Бозе-газов при 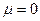 :
:
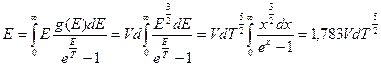 .
.
Следовательно 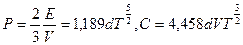 .
.
49. Найти внутреннюю энергию и давление сильно вырожденного Ферми-газа.
Решение: Как было указано ранее (см. зад. 5 и 7):
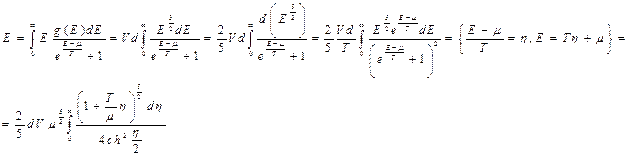
Т.к. 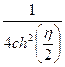 имеет резкий максимум вблизи нуля, то последний интеграл равен
имеет резкий максимум вблизи нуля, то последний интеграл равен 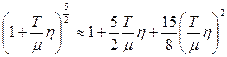 .
.
Интеграл 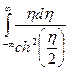 равен нулю, поэтому остается:
равен нулю, поэтому остается:
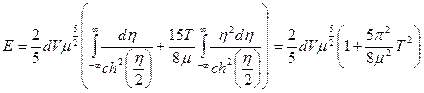
(интегралы были написаны ранее)
Учтем ранее полученную зависимость 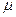 от
от 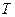 (см. зад. 3):
(см. зад. 3): 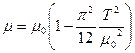 .
.
Следовательно 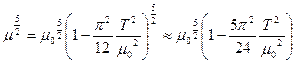 , и
, и
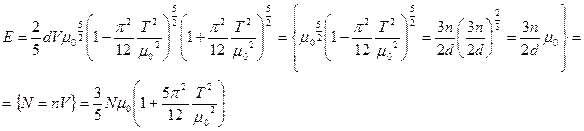
Давление 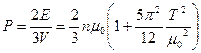 .
.
В частности, при 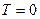
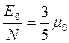 ,
, 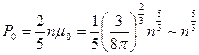
Фотонный газ. Формула Планка. Черное излучение.
Равновесное число фотонов в замкнутой полости определяется из условия:
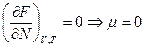 .
.
Кроме того, фотоны подчиняются статистике Бозе. Следовательно, распределение по числу частиц для них имеет вид 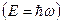
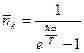
Для определения числа колебаний в заданном интервале частот достаточно взять аналогию с колебаниями в твердом теле (фононами), заменив 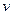 на скорость света в вакууме
на скорость света в вакууме 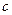 и учитывая, что
и учитывая, что 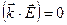 (волна поперечная, следовательно, имеется два направления поляризации электромагнитной волны). Тогда (см. теория теплоемкости тв. тела Дебая):
(волна поперечная, следовательно, имеется два направления поляризации электромагнитной волны). Тогда (см. теория теплоемкости тв. тела Дебая):
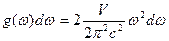
Тогда равновесное число фотонов в интервале частот 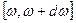
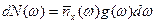 (среднее число частиц в состоянии х число состояний)
(среднее число частиц в состоянии х число состояний)
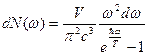 .
.
Полное число равновесных фотонов
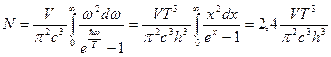 .
.
Энергия, соответствующая интервалу частот 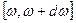
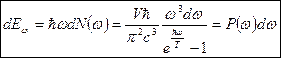 - формула Планка.
- формула Планка.
Максимум спектральной плотности при заданной температуре получается при
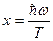
Предельные случаи
-
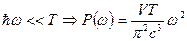 (закон Рэлея - Джинса).
(закон Рэлея - Джинса). -
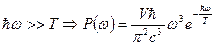 (закон излучения Вина).
(закон излучения Вина).
Полная энергия черного излучения
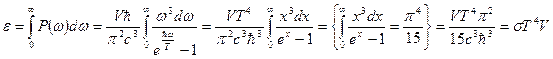 .
.
Теплоемкость фотонного газа:
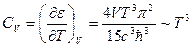 .
.
Найдем давление. Из формулы для бозонов 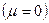 .
.
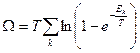
следует 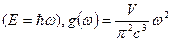 .
.
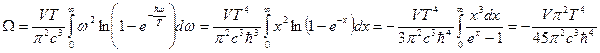
Отсюда:
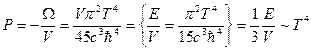 (откуда следует, что изобара и изотерма для фотонного газа суть одно и тоже)
(откуда следует, что изобара и изотерма для фотонного газа суть одно и тоже)
т.е. 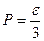 ,
,
где 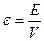 - плотность энергии.
- плотность энергии.
Энтропия
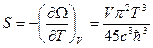 .
.
Следовательно, уравнение адиабаты фотонного газа 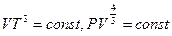 .
.
50. В предположении, что солнце излучает подобно абсолютно черному телу с температурой 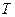 и радиусом
и радиусом 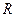 , найти мощность излучения с частотой
, найти мощность излучения с частотой 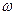 и шириной
и шириной 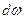 .
.
Решение: Число состояний в полосе частот 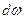 при средней частоте
при средней частоте 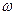 равно
равно
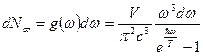
Это есть число фотонов в полости объемом 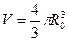 , соответствующих заданному интервалу частот. Соответствующая плотность энергии:
, соответствующих заданному интервалу частот. Соответствующая плотность энергии:
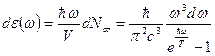 .
.
Соответствующая мощность излучения через поверхность 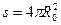 :
:
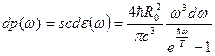 .
.
При высоких температурах 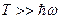 :
:
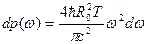 .
.
 2015-10-13
2015-10-13 2420
2420
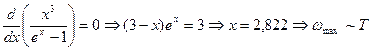 (
(