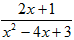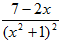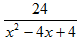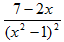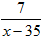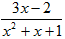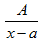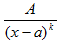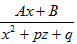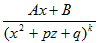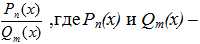 ____________________________________________________
____________________________________________________
1) рациональные функции
3) Многочлены по х степени n и m соответственно
2. Рациональная дробь вида 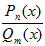 называется правильной если в ней выполняется условие:
называется правильной если в ней выполняется условие:
1) 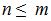 2)
2) 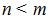 3)
3) 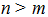 4)
4) 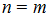
3. Укажите верное соответствие между типами простейших дробей и приведенными примерами, где a,p,q,A,B-действительные числа,k≥2, k ∈ N, p2-4q<0.
|
|
4. Выберите правильную первообразную при интегрировании дроби II типа 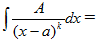 , где А и а – действительные числа, k≥2.
, где А и а – действительные числа, k≥2.
1) 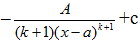 2)
2) 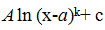 3)
3) 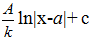 4)
4) 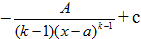
5. Представить неправильную дробь 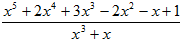 в виде суммы многочлена и правильной рациональной дроби. Выберите правильный ответ:
в виде суммы многочлена и правильной рациональной дроби. Выберите правильный ответ:
1) 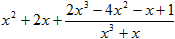 2)
2) 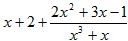
3) 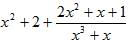 4)
4) 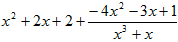
6.Найти 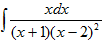 , разложив дробь на сумму простейших, и выбрать правильный ответ:
, разложив дробь на сумму простейших, и выбрать правильный ответ:
1) 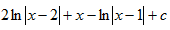 2)
2) 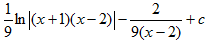
3) 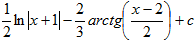 4)
4) 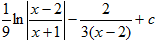
Определенный интеграл: определение, геометрический смысл, свойства. Формула Ньютона-Лейбница. Методы вычисления. Некоторые приложения определенного интеграла
- Вставьте номер пропущенного выражения, так чтобы получилось верное определение
Если существует конечный предел I интегральной суммы________составленной для функции f(x) на__________ при условии___________ и этот предел не зависит ни от способа разбиения [ a; b ] на части, ни от выбора в них промежуточных точек 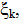 ,то функция f(x) называется интегрируемой на [ a; b ]; число I называется определенным интегралом от f(x) на [ a; b ] и обозначается символом____________________.
,то функция f(x) называется интегрируемой на [ a; b ]; число I называется определенным интегралом от f(x) на [ a; b ] и обозначается символом____________________.
1. 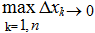 |
2. 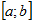 |
3. 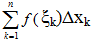 |
4. 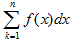 |
5. 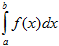 |
6. 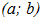 |
- Выберите среди приведенных выражений верно написанные свойства определенного интеграла, если f(x) и g(x) – интегрируемы на [ a; b ], [ a; c ], [ c; b ] k =const
1) 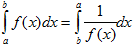 2)
2) 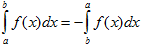 3)
3) 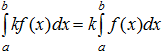
4) 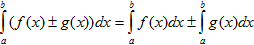
5) 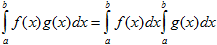
6) 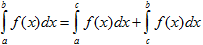
- Теорема о среднем значении определенного интеграла: если функция y=f(x) непрерывна на [ a; b ], то найдется хотя бы одна точка c є [ a; b ], в которой выполняется равенство
1) 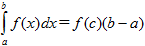 2)
2) 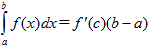 3)
3) 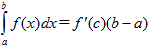
 2015-10-13
2015-10-13 1445
1445