1.Для определений уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
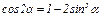 или
или 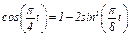 (1)
(1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
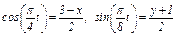 .
.
Следовательно,
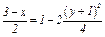
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1а):
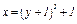 (2)
(2)
2. Скорость точки найдем по её проекциям на координатные оси:
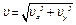 , где
, где 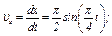
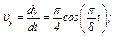
и при 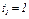 с
с
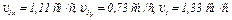 (3)
(3)
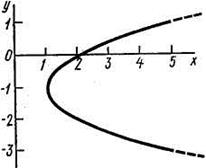
Рис. К1а
3. Аналогично найдем ускорение точки:
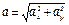 , где
, где 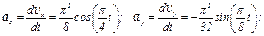
и при 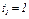 с
с
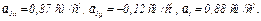 (4)
(4)
4. Касательное ускорение точки найдем, дифференцируя по времени равенство 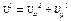 . Получим
. Получим
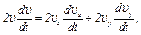
откуда
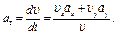 (5)
(5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив в (5) эти числа, найдем сразу, что при 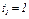 с касательное ускорение точки составит
с касательное ускорение точки составит 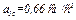 .
.
5. Нормальное ускорение точки 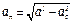 . Подставляя сюда найденные числовые значения
. Подставляя сюда найденные числовые значения 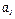 и
и 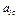 получим, что при
получим, что при 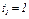 с нормальное ускорение точки составит
с нормальное ускорение точки составит 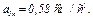
6. Радиус кривизны траектории 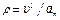 . Подставляя сюда числовые значения
. Подставляя сюда числовые значения 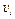 и
и 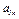 , найдем, что при
, найдем, что при 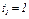 с радиус кривизны составит
с радиус кривизны составит 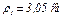 .
.
Ответ: 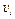 = 1,33 см/с,
= 1,33 см/с, 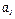 = 0,88 см/с2,
= 0,88 см/с2, 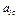 = 0,66 см/с2,
= 0,66 см/с2, 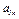 = 0,58 см/с2,
= 0,58 см/с2,
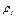 = 3,05 см.
= 3,05 см.
Пример К1б. Точка движется по дуге окружности радиуса R = 2 м по закону 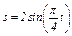 (s - в метрах, t - в секундах), где
(s - в метрах, t - в секундах), где 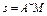 (рис. К1б). Определить скорость и ускорение точки в момент времени
(рис. К1б). Определить скорость и ускорение точки в момент времени 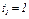 с.
с.
Решение. Определяем скорость точки:
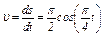 .
.
При 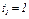 с получим
с получим 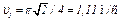
Ускорение находим по его касательной и нормальной составляющим:
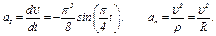
При 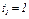 с получим, учтя, что R = 2м,
с получим, учтя, что R = 2м,
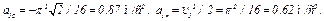
Тогда ускорение точки при 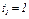 с
с
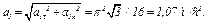
Изобразим на рис. К1б векторы 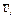 и
и 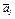 учитывая знаки
учитывая знаки 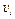 и
и 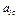 , и считая положительным направление от А к М.
, и считая положительным направление от А к М.
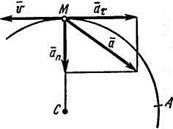
Рис. К1б
 2015-10-13
2015-10-13 921
921








