Сложные учетные ставки

Рассмотрим теперь антисипативный способ начисления сложных процентов.

Пусть

d 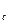(%) - сложная годовая учетная ставка;

d 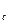- относительная величина сложной учетной ставки;

k 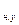- коэффициент наращения для случая учетной ставки;

f - номинальная годовая учетная ставка.

По прошествии n лет наращенная сумма составит

S = 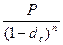. (4.1)

Отсюда для множителя наращения имеем

k = 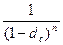. (4.2)

Так, для периода начисления, не являющегося целым числом, имеем

k = 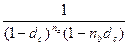. (4.3)

При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма превращается в

S = P / 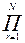(1 - n 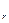d 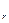). (4.4)

Здесь 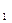n , n 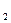, …, n 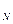- продолжительность интервалов начисления в годах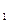, d , d 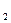,..., d 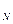- учетные ставки, соответствующие данным интервалам.

Для начисления процентов m раз в году формула имеет такой вид:

S = Р / (1 – f / m) 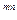(4.5)

или

S = Р / 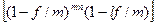(4.6)

При этом mn - целое число интервалов начисления за весь период начисления, l - часть интервала начисления.

При непрерывном начислении процентов S рассчитывается по формуле:

S = Р / 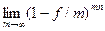(4.7)

Из полученных формул путем преобразований получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки:

 P = S (1 - d 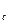) 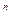; (4.8)

n = 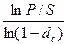; (4.9)

n = 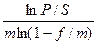; (4.10)

d 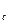= 1 - 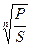; (4.11)

f = m 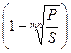. (4.12)