Проверка гипотез по двум выборкам

Пусть, после проведения экономических реформ снова был произведен опрос о заработной плате. Получены новые данные: 600,600,1300,1100,3700,1600,1100,800.

Необходимо выяснить, привели ли реформы к росту благосостояния населения.

Сформулируем гипотезы:

H₀: μ₁ = μ₂ ‑ средняя заработная плата до реформ равна средней зарплате после реформ.

H₁: μ₁ < μ₂ ‑ средняя заработная после реформ больше, чем средняя зарплата до реформ

¨ Выбор уровня значимости (вероятности ошибки).

α =0.01

¨ Выбор теста.

t критерий Стьюдента для двух выборок:

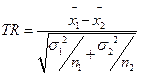(1.2)

Число степеней свободы:

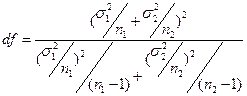(1.3)

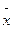‑ среднее значение выборки, σ ‑ среднеквадратическое отклонение, n – количество данных в выборке.

¨ Выполнение необходимых вычислений.

Вычислим t расчетное (TR):

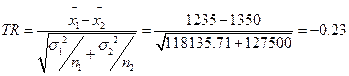
Число степеней свободы:

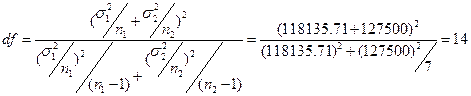
¨ Определение критической области.

Для определения критической области рассчитаем число степеней свободы t (14, 0.01)=2.977 [t(n-1, α/2)].

Правило принятия (отвержения) гипотезы: если TR < -2.977, то отвергается H₀ и принимается H₁.

Поскольку -0.23>-2.977, то нулевая гипотеза не отвергается, по вероятности ошибки 0.01. Следовательно, средняя заработная плата до проведения реформ равна средней заработной плате после проведения реформ. Таким образом, проведенные реформы не привели к существенному росту благосостояния населения.