Наряду с вращательным эффектом пары сил можно ввести понятие о вращательном эффекте силы, который она оказывает относительно точки.
Вращательный эффект силы относительно заданной точки, определяется тремя параметрами:
- плоскостью действия;
- направлением поворота;
- величиной момента, который равен произведению модуля силы на плечо, т.е. кратчайшее расстояние между точкой и силой.
Из рис. 1.24 имеем:
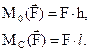
Из рис. 1.24 следует, что момент силы 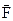 относительно центра 0 можно определить через удвоенную площадь треугольника 0AB, т.е.
относительно центра 0 можно определить через удвоенную площадь треугольника 0AB, т.е.
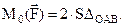
При повороте против часовой стрелки момент считается положительным; при повороте по часовой стрелке – отрицательным.
Следует иметь в виду, что любая одна сила не может вызвать реальный поворот тела. В действительности поворот тела всегда происходит под действием пары сил, одной из сил которой является та сила, момент которой мы и вычисляем.
 Теорема Вариньона. Если система сил имеет равнодействующую, то ее момент относительно любой точки равен алгебраической сумме моментов всех заданных сил относительно той же точки.
Теорема Вариньона. Если система сил имеет равнодействующую, то ее момент относительно любой точки равен алгебраической сумме моментов всех заданных сил относительно той же точки.
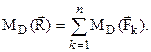
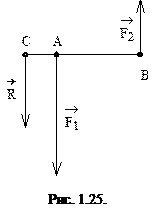
Применительно к равнодействующей двух антипаралллельных сил можно записать (рис. 1.25):
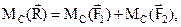
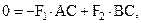
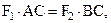
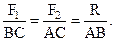
Данный результат совпадает с (1.9), полученным на основе аксиом.
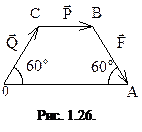 Пример 1.2. Определить момент равнодействующей сил
Пример 1.2. Определить момент равнодействующей сил 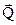 ,
, 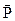 ,
, 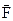 относительно точки 0, если
относительно точки 0, если 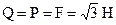 , 0A=40 см (рис. 1.26).
, 0A=40 см (рис. 1.26).
Решение. По теореме Вариньона можно записать: 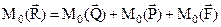 . Так как
. Так как 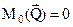 , то момент сил
, то момент сил 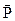 и
и 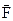 относительно точки 0 равен удвоенной площади трапеции, составленной силами
относительно точки 0 равен удвоенной площади трапеции, составленной силами 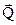 ,
, 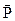 ,
, 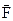 и отрезком
и отрезком 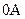 . Тогда
. Тогда
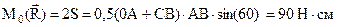
(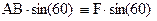 )
)
 Теорема о параллельном переносе силы. Действие силы на тело не изменится, если силу перенести параллельно самой себе в любую точку тела, добавив при этом пару сил, момент которой равен моменту заданной силы относительно новой точки приложения.
Теорема о параллельном переносе силы. Действие силы на тело не изменится, если силу перенести параллельно самой себе в любую точку тела, добавив при этом пару сил, момент которой равен моменту заданной силы относительно новой точки приложения.
Для доказательства теоремы на основе аксиомы 2 приложим в точке В две уравновешенные силы 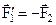 , причем
, причем 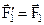 (рис. 1.27). Тогда можно считать, что к телу приложена заданная сила не в точке А, а в точке В, а силы,
(рис. 1.27). Тогда можно считать, что к телу приложена заданная сила не в точке А, а в точке В, а силы, 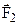 создают пару сил, момент которых равен моменту силы F1 относительно точки В, т.е.
создают пару сил, момент которых равен моменту силы F1 относительно точки В, т.е.
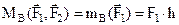 .
.
 2015-10-14
2015-10-14 412
412








