2015-10-14
939
Найдем такую точку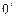 
, в которой заданная система сил приводится к равнодействующей (рис. 1.30).
Воспользуемся теоремой о параллельном переносе силы.
Перенесем главный вектор в точку 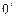, при этом расстояние 
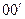выберем из условия:
 .
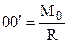| (1.16) |
Силу R в точке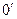 
обозначим 
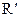и добавим присоединенный момент
 .
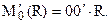| (1.17) |
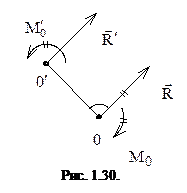Из сравнения (1.16) и (1.17) следует, что главный момент 
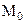и присоединенный момент 
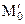равны по величине и противоположны по направлению, т.е. в сумме они дают 0. Следовательно 
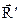является равнодействующей данной системы сил.
Очевидно, изложенный метод может быть применен всегда, т.е. произвольную плоскую систему сил можно привести либо к равнодействующей (случай 1), либо к паре сил (случай 2).
