Если каждому значению переменной х (аргументу) из некоторого множества Х ставится в соответствие одно значение у из множества Y, то говорят, что на множестве Х задана функция f (x)со множеством значений Y, где Х – область определения функции, Y – область значения функции, или у является функцией от х и записывают у = f(x). Если функция задана аналитически, то областью существования функции (иначе, областью значения функции) называется совокупность тех действительных значений аргумента, при которых аналитическое выражение определяющее функцию, принимает только действительные значения.
Графиком функции у = f(x) называется множество точек (х, f(x)). Графиком пользуются для геометрического изображения функций. Графики многих функций строят с помощью параллельного переноса, растяжения или сжатия основных элементарных функций: степенной, показательной, логарифмической, тригонометрической и обратных тригонометрических.
Функция у = f(x) называется четной, если выполняется равенство  . График четной функции симметричен относительно оси ординат. Функция у = f(x) называется нечетной, если выполняется равенство
. График четной функции симметричен относительно оси ординат. Функция у = f(x) называется нечетной, если выполняется равенство  . График нечетной функции симметричен относительно начала координат.
. График нечетной функции симметричен относительно начала координат.
Пример: Найти область значения функции:

Решение:
 .
.
Предел функции.
Число А называется пределом функции при х  , если для любого сколь угодно малого
, если для любого сколь угодно малого  существует число
существует число  такое, что
такое, что  при
при 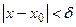 . Это записывают так:
. Это записывают так:  . Аналогично определяется предел при х
. Аналогично определяется предел при х  .
.
Функция  называется бесконечно большой при х
называется бесконечно большой при х  , если
, если  и бесконечно малой при х
и бесконечно малой при х  , если
, если 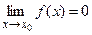 . Аналогично определяются бесконечно большие и бесконечно малые при х
. Аналогично определяются бесконечно большие и бесконечно малые при х  .
.
При вычислении пределов необходимо знать такие теоремы:
 - Const.
- Const.
Если 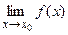 и
и 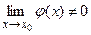 существуют, то
существуют, то 



Для всех основных элементарных функций в произвольной точке их области определения справедливо равенство 

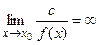 ;
;

 Const.
Const.
5.  ,
, 


Бесконечно малые  и
и  называются эквивалентными при х
называются эквивалентными при х  , если
, если  . Это записывают так:
. Это записывают так: 
Если  при
при  , то выполняются эквивалентности:
, то выполняются эквивалентности:
1.  4.
4. 
2.  5.
5. 
3.  6.
6. 
Предел отношений двух бесконечно малых не изменится, если заменить их эквивалентными величинами.
При вычислении пределов часто используют:
 2015-10-22
2015-10-22 3225
3225
