Простейшее уравнение параболы

y²= 2 px

Входящая в это уравнение величина р называется параметром параболы. Параметр параболы равен расстоянию от директрисы параболы до ее фокуса.

Координаты фокуса F параболы F(, 0). Уравнение директрисы параболы

. Эксцентриситет параболы е= 1.

Пример. Составить простейшее уравнение гиперболы, если расстояние между вершинами ее равно 20, а расстояние между фокусами 30.

Решение:

Вершины гиперболы лежат на ее действительной оси. По условию 2а = 20; 2с == 30. Значит, а = 10; с = 15 а² = 100; с² = 225.

Величины а, и и с у гиперболы связаны соотношением а² +b² = с²; отсюда

b ² = с² —а² = 225 — 100 Þ b ² = 125. Значит, уравнением гиперболы будет

Пример. Действительная полуось гиперболы равна 5, эксцентриситет е= 1,4. Найти уравнение гиперболы.

Решение:

По условию а = 5, значит а² = 25. По формуле е = =1,4, отсюда с = 1,4·а = 1,4 · 5 = 7; с ² = 49; b ² = с ² - а² = 49 — 25 = 24, b ² =24

Иско­мым уравнением будет

Пример. Найти уравнение асимптот гиперболы 2 x² - 3 y² = 6.

Решение:

У гиперболы две асимптоты, определяемые урав­нениями Следует найти a и b.

Приведем уравнение гиперболы к простейшему виду, разде­лив обе его части на 6. Получим

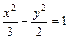
Отсюда заключаем, чт а² =. 3, а = ; b ² = 2, b == . Подстав­ляя эти значения а и b в уравнения асимптот получаем: ;