2015-10-22
436
Полное исследование функции проводится по следующему плану.
1) Найти область определения функции 
.
2) Проверить наличие у исследуемой функции дополнительных свойств (четность, нечетность, периодичность). В случае, когда, например, функция является нечетной (четной), достаточно проводить исследования и строить эскиз графика при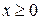 
с последующим симметричным его отображением (относительно начала координат для нечетной функции или относительно оси 
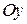для четной).
3) Определить координаты точек пересечения графика функции с осями координат (для нахождения точки пересечения графика с осью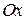 
решаем уравнение 
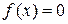; для нахождения точки пересечения графика с осью 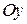подставляем в аналитическое выражение функции значение 
).
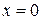4) Найти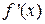 
и с ее помощью определить интервалы монотонности функции, точки экстремума и экстремальные значения функции.
5) Найти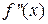 
, с ее помощью определить направления выпуклости графика функции и найти точки перегиба графика функции.
6) Найти асимптоты графика.
7) Используя все полученные результаты, построить график функции.
