Пусть функция  имеет конечную или бесконечную производную в каждой точке интервала
имеет конечную или бесконечную производную в каждой точке интервала 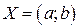 . Обозначим
. Обозначим 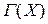 дугу графика функции
дугу графика функции 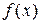 , соответствующую интервалу
, соответствующую интервалу 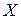 .
.
Определение. Если дуга 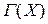 лежит не ниже (не выше) касательной к графику функции
лежит не ниже (не выше) касательной к графику функции  , проведенной в любой точке
, проведенной в любой точке 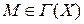 , то функция или график функции называется выпуклым вниз (соответственно выпуклым вверх) в интервале
, то функция или график функции называется выпуклым вниз (соответственно выпуклым вверх) в интервале 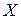 (рис. 6 а).
(рис. 6 а).
Точка на графике функции, в которой существует касательная к графику функции, называется точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости (рис. 6 б,в).
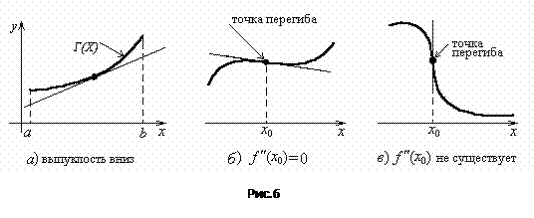
Заметим, что в точке перегиба требуется существование касательной к графику.
В некоторых учебных пособиях выпуклую вверх функцию называют вогнутой, а выпуклую вниз функцию - выпуклой. Мы будем также пользоваться этими терминами, когда это удобно.
Теорема (достаточное условие выпуклости вверх и вниз). Если функция 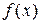 дифференцируема дважды в интервале
дифференцируема дважды в интервале 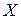 и в ней
и в ней 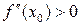 (
(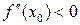 ), то
), то 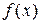 является выпуклой вниз (соответственно выпуклой вверх) в интервале
является выпуклой вниз (соответственно выпуклой вверх) в интервале 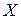 .
.
|
|
|
Необходимое условие точки перегиба. Если 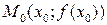 - точка перегиба функции
- точка перегиба функции 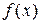 , то либо и
, то либо и 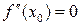 , либо
, либо 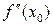 не существует (рис. б, в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.
не существует (рис. б, в). Следовательно, абсциссы точек перегиба нужно искать в тех значениях x, при которых вторая производная либо равна нулю, либо не существует.
Достаточное условие точки перегиба. Пусть функция 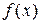 имеет производную (может быть бесконечную) в точке
имеет производную (может быть бесконечную) в точке  , существует вторая производная в проколотой окрестности точки
, существует вторая производная в проколотой окрестности точки  и либо
и либо 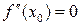 , либо
, либо 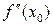 не существует. Тогда если при переходе через
не существует. Тогда если при переходе через 
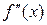 меняет знак, то
меняет знак, то 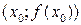 является точкой перегиба.
является точкой перегиба.
При решении задач на поиск точек перегиба графика функции одного переменного придерживаются следующей схемы рассуждений
1) Установить область определения функции  .
.
2) Найти вторую производную 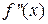 .
.
3) Выяснить, в каких точках из области определения вторая производная обращается в нуль (т.е. решить уравнение 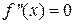 ) или не существует.
) или не существует.
4) Установить знак второй производной на числовых интервалах, на которые найденные точки разбили область определения, и определить направления выпуклости (если 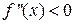 , то график функции направлен выпуклостью вверх, т.е. Ç; если
, то график функции направлен выпуклостью вверх, т.е. Ç; если 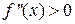 - выпуклостью вниз, т.е. È).
- выпуклостью вниз, т.е. È).
5) Если при переходе через найденную точку  направление выпуклости меняется, то точка
направление выпуклости меняется, то точка 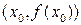 – точка перегиба графика функции.
– точка перегиба графика функции.
 2015-10-22
2015-10-22 2616
2616
