Определение. Прямая  называется асимптотой кривой
называется асимптотой кривой  , если расстояние от точки
, если расстояние от точки  кривой до прямой
кривой до прямой  стремится к нулю при неограниченном удалении этой точки по кривой от начала координат (т.е. стремление хотя бы одной из координат точки к бесконечности). Пример показан на рис. 7 а.
стремится к нулю при неограниченном удалении этой точки по кривой от начала координат (т.е. стремление хотя бы одной из координат точки к бесконечности). Пример показан на рис. 7 а.
Нахождение вертикальных асимптот. Если  - точка разрыва II рода функции
- точка разрыва II рода функции  , то прямая
, то прямая  является вертикальной асимптотой. Например, если
является вертикальной асимптотой. Например, если  то точка графика при
то точка графика при 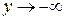 бесконечно близко приближается к вертикальной асимптоте
бесконечно близко приближается к вертикальной асимптоте  с левой стороны (рис. 7 в,
с левой стороны (рис. 7 в,  ).
).
 |
Вертикальная асимптота может быть в точке, являющейся границей области определения функции, если односторонний предел в этой точке равен  или
или  (рис. 7 в).
(рис. 7 в).
Нахождение горизонтальных асимптот. Если  (или
(или  ), то прямая
), то прямая 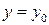 является горизонтальной асимптотой при
является горизонтальной асимптотой при  (или
(или 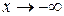 ).
).
Нахождение наклонных асимптот. Уравнение наклонной асимптоты имеет вид  , где угловой коэффициент
, где угловой коэффициент 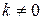 . Коэффициенты
. Коэффициенты  и
и 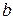 при
при  (
(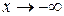 ) находят по формулам:
) находят по формулам:
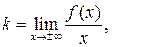
 .
.
Замечание. В формулах подразумевается, что оба предела существуют и конечны. Если хотя бы один из них не существует, то наклонной асимптоты у графика функции нет.
Замечание. Если пределы конечны и  , то график имеет горизонтальную асимптоту
, то график имеет горизонтальную асимптоту 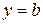 при
при  (
(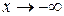 ). Поэтому если существует горизонтальная асимптота при
). Поэтому если существует горизонтальная асимптота при  (
(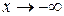 ), то нет наклонной асимптоты при
), то нет наклонной асимптоты при  (
(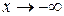 ).
).
 2015-10-22
2015-10-22 4017
4017








