2015-10-22
542
Пример 1. Найти наибольшее и наименьшее значения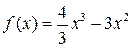 
на отрезке 
.
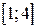Решение.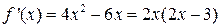 
, причем производная определена всюду, критических точек нет. Чтобы найти стационарные точки, приравниваем производную к нулю: 
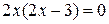. Итак, 
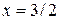и 
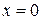– стационарные точки. При этом 
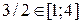, а 
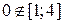, поэтому последняя точка нас не интересует. Вычисляем значения исходной функции в выбранной точке и на концах отрезка: 
; 
; 
.
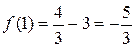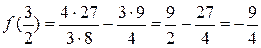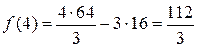Сравнивая значения, получаем: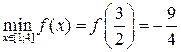 
, 
.
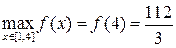Пример 2. Найти наибольшее и наименьшее значения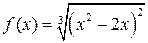 
в интервале 
.
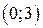Решение.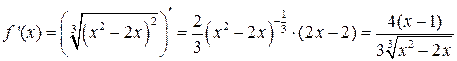 
, причем производная не существует пр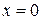и и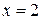 
. Эти точки являются критическими. Чтобы найти стационарные точки, приравниваем производную к нулю: 
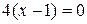, т.е. 
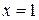. Итак, 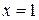- стационарная точка. При этом 
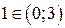и 
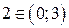, а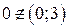 
, поэтому последняя точка нас не интересует. Вычисляем значения исходной функции в выбранных точках:
, 
.
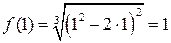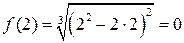Находим предельные значения функции на границах интервала:
;
.
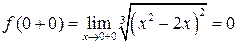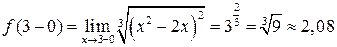Эти значения в точках 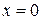и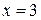 
функция не достигает, поскольку эти точки не принадлежат интервалу .
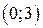Сравнивая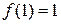 
, 
, 
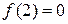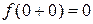и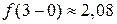 
, получаем 
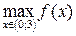не существует, 
.
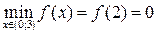При решении задач практического характера полезно пользоваться следующим фактом.
Пусть функция 
определена на открытом числовом интервале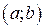 
и имеет на нем единственную стационарную точку 
. Если – точка локального максимума, то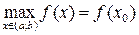 
; если - точка локального минимума, то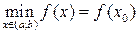 
Пример 3. Определить наибольшую площадь равнобедренного треугольника, вписанного в круг радиуса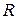 
.
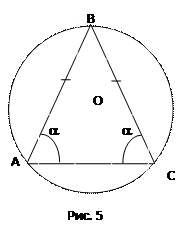
Решение. Пусть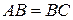 
и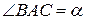 
, тогда 
, 
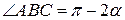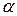– острый угол. Из теоремы синусов имеем
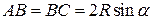, а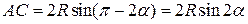 
.
.
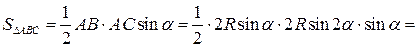
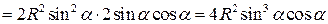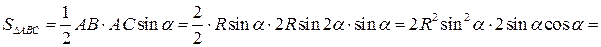
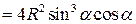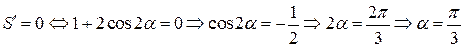– стационарная точка функции 
.
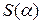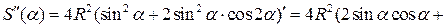
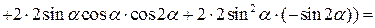
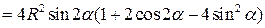
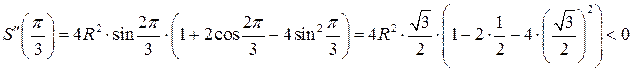
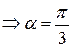– точка локального максимума, так как функция 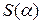непрерывна на 
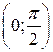и имеет единственную точку локального максимума, то в этой точке обязательно достигается наибольшее значение функции на этом интервале. Найдем 
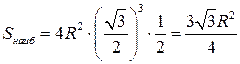(кв.ед.)
