2015-10-22
300
Пример 1. Провести полное исследование функции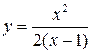 
Решение.
1) 
.
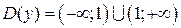2) 
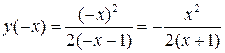, т.е. 
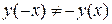и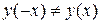 
. Функция является функцией общего вида, непериодической.
3) Так как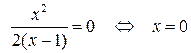 
, то график пересекает оси координат только в точке 
.
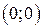4) 
.
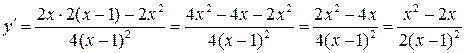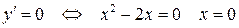или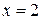 
. 
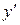не существует в точке 
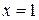, но она не входит в область определения функции. Следовательно, имеются две стационарные точк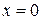и 
и 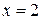. Разобьем этими точками область определения на интервалы знакопостоянства производной: 
, 
, 
, 
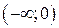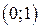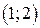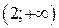. Определим знаки производной в этих интервалах (см. рис. 8).
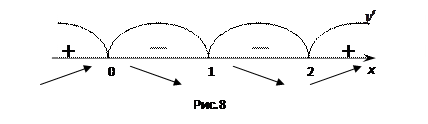
Используя достаточные условия монотонности и экстремума, можно сделать следующие выводы: функция возрастает в интервалах 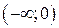и 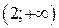, убывает в 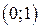и 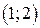. Значение максимума 
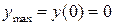, значение минимума 
.
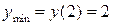5) 
.
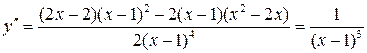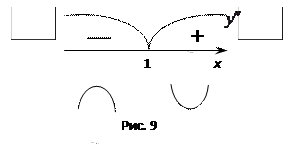
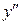не обращается в 0, а в точке 1, где 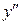не существует, функция не определена, поэтому график функции не имеет точки перегиба. Таким образом, имеются два интервала 
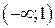и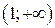 
, знакопостоянства второй производной (см. рис.9).
В силу достаточных условий выпуклости и вогнутости графика в интервале 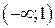график выпуклый (вверх), а в интервале 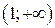график вогнутый (выпуклый вниз).
6)Так как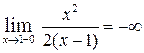 
, 
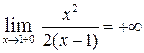, то прямая 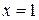– вертикальная асимптота графика функции.
.
.
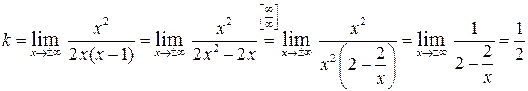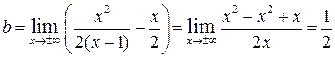Следовательно, прямая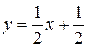 
– наклонная асимптота графика функции при 
.
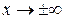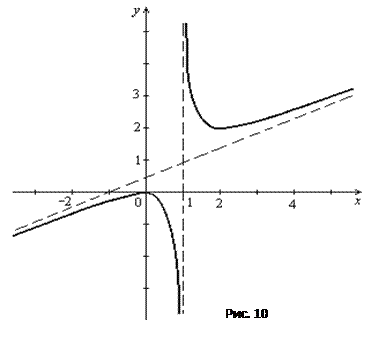
7) Построим график функции. Сначала изобразим асимптоты 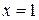и 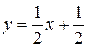(пунктирной линией). Наносим на чертеж точки (0, 0) и (2, 2), найденные в пункте 4. Проводим через эти точки линию, согласно результатам исследования функции в пунктах 4, 5, 6. Еще раз сравниваем полученный график с результатами исследования и убеждаемся в правильности построения графика.
