2015-10-22
478
Пусть имеется l нормально распределенных совокупностей, дисперсии которых равны соответственно 
и l независимых выборок из каждой совокупности объемов 
. Необходимо проверить нулевую гипотезу о равенстве дисперсий, то есть 
или 
(i=1,2,… l).
Для проверки гипотезы 
может быть использован критерий Бартлетта. Доказано, что при справедливости гипотезы и при условии, что 
статистика:
;
- исправленная выборочная дисперсия i-й выборки,
- оценка средней арифметической дисперсии имеет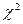 
- распределение с l-1 степенями свободы. Поэтому гипотеза отвергается, если фактически наблюдаемое значение 
, где 
- критическое значение критерия 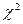, найденное на уровне значимости 
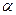при числе степеней свободы l-1.
Таким образом, критерии проверки гипотез о равенстве дисперсий двух или более совокупностей можно представить в виде таблицы.
| Нулевая гипотеза | Предполо-жения | Статистика критерия | Альтернативная гипотеза | Критерий отклонения гипотезы |
| 
неиз-вестны
| 
| 
| 
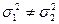
или 
|
