Для установления теоретического закона распределения случайной величины Х по опытным данным (эмпирическому распределению) необходимо определить вид и параметры закона распределения. Критерием согласия называется критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Пусть необходимо проверить нулевую гипотезу H0 о том, что исследуемая случайная величина Х подчиняется определенному закону распределения. Для проверки гипотезы H0 выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения. Зная закон распределения U, можно найти такое критическое ее значение uкр, что вероятность 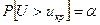 мала. Поэтому, если наблюдаемое значение
мала. Поэтому, если наблюдаемое значение 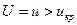 , гипотезу H0 отвергают, в противном случае H0 принимают.
, гипотезу H0 отвергают, в противном случае H0 принимают.
С помощью критерия согласия (Пирсона) можно проверить гипотезу о различных законах распределения генеральной совокупности (равномерном, нормальном, показательном и др.) Для этого в предположении о конкретном виде распределения вычисляются теоретические частоты 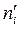 , и в качестве критерия выбирается случайная величина
, и в качестве критерия выбирается случайная величина
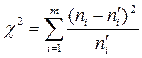 ,
,
имеющая закон распределения χ 2 с числом степеней свободы k = m – 1 – r, где m – число частичных интервалов выборки, r – число параметров предполагаемого распределения. Критическая область выбирается правосторонней, и граница ее при заданном уровне значимости α  находится по таблице критических точек распределения χ 2.
находится по таблице критических точек распределения χ 2.
Теоретические частоты 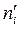 вычисляются для заданного закона распределения как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения, параметры которого совпадают с их точечными оценками по выборке, а именно:
вычисляются для заданного закона распределения как количества элементов выборки, которые должны были попасть в каждый интервал, если бы случайная величина имела выбранный закон распределения, параметры которого совпадают с их точечными оценками по выборке, а именно:
а) для проверки гипотезы о нормальном законе распределения 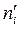 = п ∙ Рi, где п – объем выборки,
= п ∙ Рi, где п – объем выборки, 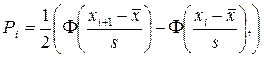 xi и xi + 1 – левая и правая границы i -го интервала,
xi и xi + 1 – левая и правая границы i -го интервала, 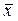 - выборочное среднее, s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3;
- выборочное среднее, s – исправленное среднее квадратическое отклонение. Поскольку нормальное распределение характеризуется двумя параметрами, число степеней свободы k = n – 3;
б) для проверки гипотезы о показательном распределении генеральной совокупности в качестве оценки параметра λ принимается 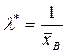 . Тогда теоретические частоты
. Тогда теоретические частоты 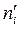 = п ∙ Рi,
= п ∙ Рi, 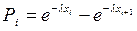 . Показательное распределение определяется одним параметром, поэтому число степеней свободы k = n – 2;
. Показательное распределение определяется одним параметром, поэтому число степеней свободы k = n – 2;
в) для проверки гипотезы о равномерном распределении генеральной совокупности концы интервала, в котором наблюдались возможные
значения Х, оцениваются по формулам:

Тогда плотность вероятности 
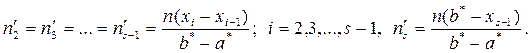
Число степеней свободы k = n – 3, так как равномерное распределение оценивается двумя параметрами.
Пример.
Для выборки, интервальный статистический ряд которой имеет вид
| Номер интервала | Границы интервала | Эмпирические частоты |
| 2 – 5 | ||
| 5 – 8 | ||
| 8 – 11 | ||
| 11 – 14 | ||
| 14 – 17 | ||
| 17 – 20 |
проверить при уровне значимости α = 0,05 гипотезу о:
а) показательном; б) равномерном; в) нормальном
законе распределения генеральной совокупности с помощью критерия Пирсона.
Решение.
Объем выборки п = 70. Будем считать вариантами середины частичных интервалов: х 1 = 3,5, х 2 = 6,5,…, х 6 = 18,5.
Найдем  = 11,43; σВ = 4,03; s = 4,05.
= 11,43; σВ = 4,03; s = 4,05.
а) Вычислим теоретические частоты в предположении о показательном распределении генеральной совокупности при 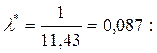
 аналогично
аналогично 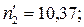
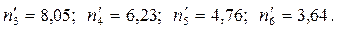 Наблюдаемое значение критерия
Наблюдаемое значение критерия  Критическая точка χ 2(0,05;4)=9,5;
Критическая точка χ 2(0,05;4)=9,5;  и гипотеза о показательном распределении отклоняется.
и гипотеза о показательном распределении отклоняется.
б) Для равномерного распределения 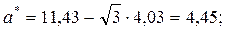
 теоретические частоты:
теоретические частоты: 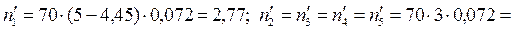
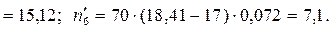 Наблюдаемое значение критерия
Наблюдаемое значение критерия  Критическая точка
Критическая точка 
 и гипотеза о равномерном распределении отклоняется.
и гипотеза о равномерном распределении отклоняется.
в) Теоретические частоты для нормального распределения:

 Так же вычисляются
Так же вычисляются 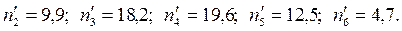 Наблюдаемое значение критерия
Наблюдаемое значение критерия  Критическая точка
Критическая точка  Поскольку
Поскольку  гипотеза о нормальном распределении генеральной совокупности принимается.
гипотеза о нормальном распределении генеральной совокупности принимается.
 2015-10-22
2015-10-22 1491
1491
