Координаты вектора, заданного точками

Если известны координаты точек А(х₁;у₁;z₁) и В(х₂;у₂;z₂), то координаты вектора равны разностям соответствующих координат его конца и начала: .

Пример 1. Даны точки А₁(2; -1; -2), А₂(1; 2; 1). Найти модуль вектора и направляющие косинусы.

Решение.

Найдем координаты вектора . Находим модуль и направляющие косинусы , , , .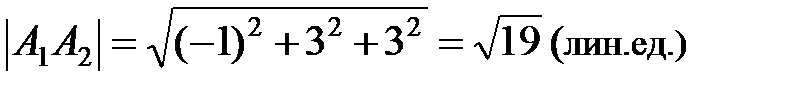

Пример 2. Векторы 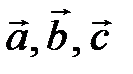заданы в пространстве своими координатами. , , .

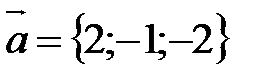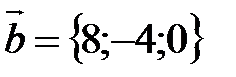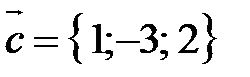Найти: длину вектора .

Решение.

Найдем векторы: , , .

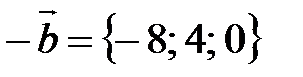Выполним сложение:

.

Найдем модуль (длину) полученного вектора

лин. ед.

Задания для самостоятельной работы.

1. Векторы 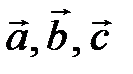заданы в пространстве своими координатами. Найти длину вектора .

а)	б)
в)	г)

2. № 372, № 373, № 387, № 398, № 396 [6]

3. № 749 – 752, № 754, № 758, № 775 – 778, № 782, № 785 [5]

Рекомендуемая литература: [7] стр. 39-45, [4] стр. 70-78.

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5