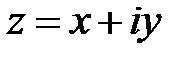Различные формы комплексных чисел

- алгебраическая форма комплексного числа.

- тригонометрическая форма комплексного числа, где r - модуль, φ - аргумент комплексного числа.

показательная форма комплексного числа.

Пример 1. Записать в тригонометрической и показательной форме следующие комплексные числа: а) ; б) ; в) .

Решение.

а)

Изобразим данное число на комплексной плоскости (рис. 11).

z=1+i

х

у

i

О

Рисунок 11

Найдем модуль и аргумент этого комплексного числа.

Аргумент комплексного числа удобно определить из формул:

Угол, для которого , находится в первой четверти .

Итак, данное число можно записать в следующей тригонометрической форме .

Показательная форма: .

б) z=-2; x=-2; y = 0. (рис. 12).

Тригонометрическая форма данного числа: .

х

у

3i

О

-2

Рисунок 12

Показательная форма: .

в) (рис. 12).

Тригонометрическая форма: .

Показательная форма: .

Пример 2. Дано комплексное число .

1) Записать это число в алгебраической, тригонометрической и показательной формах.

Решение.

1) Чтобы записать число z в алгебраической форме , умножим числитель и знаменатель на число, сопряженное знаменателю

.

Итак, алгебраическая форма числа: .

Запишем данное число в тригонометрической форме .

z=1/2-1/2i

х

у

1/2

-1/2i

О

Рисунок 13

Имеем . Получим ,

Угол, для которого косинус положителен, а синус отрицателен, находится в четвертой четверти. В этом можно убедиться, если изобразить данное число на комплексной плоскости (рис. 13). Следовательно, .

Число z в тригонометрической форме запишется в виде .

Показательная форма: .