Свойства сходящихся числовых рядов

1) Если ряд сходится и имеет сумму S, то ряд сходится и имеет сумму CS.

2) Если ряды и сходятся и имеют суммы и соответственно, то сходятся и ряды и имеют суммы .

3) Добавление и отбрасывание конечного числа слагаемых не влияет на характер сходимости ряда.

Знакоположительные ряды. Необходимый признак сходимости.

Теорема. Если ряд сходится, то .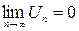

Обратное утверждение неверно: если 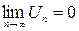, то ряд может и сходиться и расходиться.

Следствие (достаточный признак расходимости ряда):

Если , то ряд расходится.

Примеры.

1) – ряд расходится.

2) – ничего нельзя сказать о характере сходимости ряда. Нужны дополнительные исследования с помощью других признаков.