Достаточные признаки сходимости знакоположительных рядов

1 Признак сравнения.

Даны два знакоположительных ряда и . Пусть, начиная с некоторого n, может быть и с n= 1, выполняется 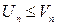, тогда:

а) если сходится, то сходится и ;

б) если расходится, то расходится и .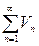

Следствие: если существует , конечное число, то ряды сходятся или расходятся одновременно.

Для использования этого признака удобно выбирать ряд, составленный из членов геометрической прогрессии , который сходится при и расходится при , а также обобщенный гармонический ряд , который сходится при и расходится при .

2 Признак Даламбера.

Пусть и существует . Тогда при q <1 ряд сходится, при q >1 – расходится, при q =1 – сомнительный случай (нужно исследовать с помощью других признаков).

3 Радикальный признак Коши.

Пусть и существует 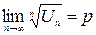. Тогда при p <1 ряд сходится, при p >1 – расходится, при p =1 – сомнительный случай.

4 Интегральный признак Коши.

Дан знакоположительный ряд

(1)

Пусть 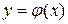– непрерывная, положительная, монотонно убывающая функция, определенная при и такова, что члены ряда являются значениями функции при , т. е. , , …, ,…, тогда ряд (1) и несобственный интеграл сходятся или расходятся одновременно.

План исследования знакоположительных рядов

1. Находим . Если 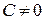, то ряд расходится, исследование закончено.

2. Если , применяем один (подходящий) из достаточных признаков сходимости.

3. Делаем вывод о сходимости ряда.

Примеры.

Напоминаем, что

; 0!=1;

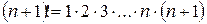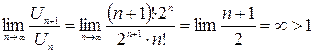– ряд, расходящийся по признаку Даламбера.

2) – ряд сходится по радикальному признаку Коши.

3) сравним с 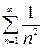– сходящимся (как обобщенный гармонический при k >1). Используем следствие из признака сравнения: – конечное, не равное нулю число, тогда ряды ведут себя одинаково, т. е. сходятся.

Знакопеременные ряды

Это ряды, содержащие как положительные, так и отрицательные члены. Частным случаем таких рядов являются знакочередующиеся ряды: ряды, в которых за каждым положительным членом следует отрицательный и за каждым отрицательным членом следует положительный:

или

Признак Лейбница.

Если в знакочередующемся ряде

1) абсолютные величины членов ряда убывают ;

2) ,

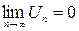то знакочередующийся ряд сходится и его сумма не превосходит модуля первого члена.

Следствие. Пусть знакочередующийся ряд сходится по признаку Лейбница. Если сумму этого ряда заменить суммой n первых членов, то погрешность, допускаемая при этом не превосходит модуля первого отброшенного члена.

Рассмотрим знакочередующийся ряд и ряд, составленный из абсолютных его величин. Если ряд, составленный из абсолютных величин, сходится, то знакопеременный ряд называется абсолютно сходящимся рядом. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин, расходится, то знакопеременный ряд называется условно сходящимся.

Пример. Исследовать на условную и абсолютную сходимость ряд.

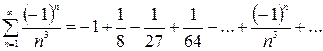
Это знакочередующийся ряд. Применим признак Лейбница.

1) ;

2) . => ряд сходится по признаку Лейбница.

Исследуем ряд на условную и абсолютную сходимость. Для этого рассмотрим ряд, составленный из абсолютных величин данного ряда.

– это обобщенный гармонический ряд, он сходится, так как k =3>1, тогда знакочередующийся ряд 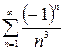является абсолютно сходящимся рядом.

Степенные ряды

Степенным рядом называется ряд вида:

где – постоянные величины, коэффициенты ряда, число a – центр ряда.

При a =0 имеем

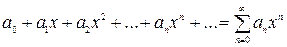
(1)

При степенной ряд (1) принимает вид

(2)

Это уже числовой ряд. он может сходиться или расходиться.

Если ряд (2) сходится, то 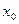– точка сходимости степенного ряда (1). Если ряд (2) расходится, то 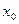– точка расходимости. Совокупность точек сходимости называется областью сходимости степенного ряда.

Теорема Абеля. Для любого степенного ряда (1) существует интервал , внутри которого ряд сходится абсолютно, вне его расходится, а на границах может иметь различный характер сходимости.

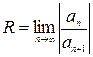– радиус интервала сходимости.

– интервал сходимости.

Если R =0, то точка x =0 – единственная точка сходимости.

Если R =¥, то ряд сходится на всей числовой оси.

Пример.

1) Найти радиус и интервал сходимости степенного ряда. Исследовать сходимость ряда на концах интервала.

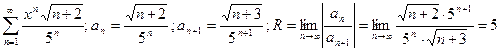Тогда (-5; 5) – интервал, внутри которого ряд сходится абсолютно. Исследуем характер сходимости ряда на границах.

1) x =–5, тогда степенной ряд примет вид

Это знакочередующийся ряд. Для него применим признак Лейбница:

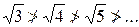– не выполнено первое условие признака Лейбница, тогда ряд

расходится, точка 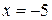– точка расходимости.

2) x =5; – ряд расходится по следствию из необходимого признака, тогда x =5 – точка расходимости.

(-5; 5) – область сходимости данного степенного ряда.

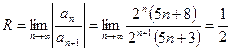– интервал сходимости данного степенного ряда. Исследуем на границах:

1) , тогда степенной ряд примет вид:

– это знакочередующийся ряд. Проверим два условия:

1) ;

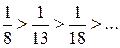2) , тогда ряд сходится по признаку Лейбница, точка – есть точка сходимости первоначального степенного ряда, она входит в область сходимости.

2) . Сравним этот ряд с гармоническим , который, как известно, расходится.

– конечное число, тогда по следствию из признака сравнения ряды ведут себя одинаково, т. е. оба расходятся, поэтому точка – точка расходимости начального степенного ряда.