Пусть  – СВ с математическим ожиданием
– СВ с математическим ожиданием 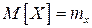 . Рассмотрим отклонение СВ
. Рассмотрим отклонение СВ  от ее математического ожидания:
от ее математического ожидания: 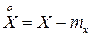 .
.
Отклонение СВ  от ее математического ожидания называется центрированной случайной величиной
от ее математического ожидания называется центрированной случайной величиной 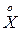 .
.
Математическое ожидание центрированной СВ равно 0: 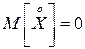 .
.
Центральным моментом k-го порядка 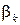 случайной величины
случайной величины  называется математическое ожидание от k- той степени соответствующей центрированной случайной величины:
называется математическое ожидание от k- той степени соответствующей центрированной случайной величины:
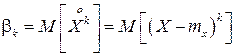 .
.
Для дискретной СВ: 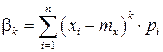 .
.
Для непрерывной СВ: 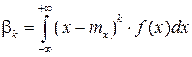 .
.
Центральный момент 1-го порядка 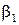 есть математическое ожидание и равен 0.
есть математическое ожидание и равен 0.
Дисперсия
Центральный момент 2-го порядка 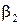 называется дисперсией случайной величины и обозначается
называется дисперсией случайной величины и обозначается 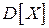 .
.
Или: дисперсией называется математическое ожидание от квадрата центрированной случайной величины.
Формулы для вычисления дисперсии:
дискретной СВ
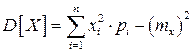 ;
;
непрерывной СВ
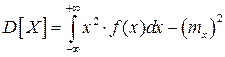 .
.
Дисперсия 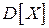 есть «среднее значение квадрата отклонения случайной величины
есть «среднее значение квадрата отклонения случайной величины  от своего среднего». Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг ее математического ожидания.
от своего среднего». Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг ее математического ожидания.
Если дисперсия СВ  конечна, то число
конечна, то число 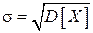 называют среднеквадратическим отклонением случайной величины
называют среднеквадратическим отклонением случайной величины  .
.
Свойства дисперсии.
Все свойства дисперсии следуют из соответствующих свойств математического ожидания.
1. 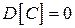 – дисперсия постоянной величины равна 0.
– дисперсия постоянной величины равна 0.
2. 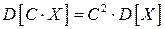
3. 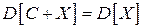
Пример. Найти дисперсию случайной величины
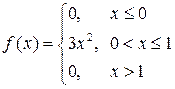 .
.
Решение. Найдем сначала математическое ожидание случайной величины:

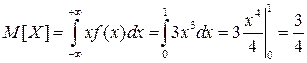 .
.
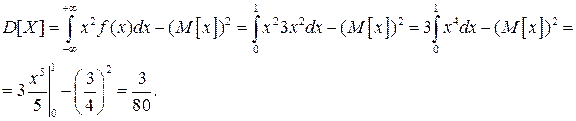
Рассмотрим центральный момент 3-го порядка 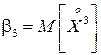 .
.
Величина 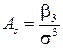 называется коэффициентом асимметрии и характеризует асимметрию (или «скошенность») распределения. Если распределение симметрично относительно математического ожидания, то
называется коэффициентом асимметрии и характеризует асимметрию (или «скошенность») распределения. Если распределение симметрично относительно математического ожидания, то 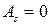 (кроме того, все центральные моменты нечетного порядка в этом случае равны 0).
(кроме того, все центральные моменты нечетного порядка в этом случае равны 0).
Эксцессом СВ называется величина
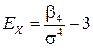 ,
,
где 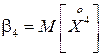 – центральный момент 4-го порядка,
– центральный момент 4-го порядка, 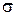 – среднеквадратическое отклонение случайной величины
– среднеквадратическое отклонение случайной величины  .
.
Число 3 вычитается потому, что для наиболее распространенного нормального распределения величина 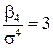 , поэтому для нормального распределения эксцесс равен 0; для кривых, более островершинных, чем кривая нормального распределения,
, поэтому для нормального распределения эксцесс равен 0; для кривых, более островершинных, чем кривая нормального распределения, 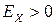 ; для кривых, менее островершинных, чем кривая нормального распределения,
; для кривых, менее островершинных, чем кривая нормального распределения, 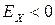 .
.
 2015-10-22
2015-10-22 1474
1474
