Итак, визуально найдено, что на отрезке  расположен один (наибольший) корень уравнения. Проверяем условие
расположен один (наибольший) корень уравнения. Проверяем условие  .
.

 , т.е. на отрезке
, т.е. на отрезке  расположен корень уравнения.
расположен корень уравнения.
1) Находим значение корня в первом приближении. Согласно методу дихотомии  . Т.к. длина отрезка
. Т.к. длина отрезка 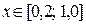
 , то точность нахождения корня недостаточна, и потребуется второе приближение. Точка
, то точность нахождения корня недостаточна, и потребуется второе приближение. Точка 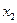 делит отрезок
делит отрезок  на две половины
на две половины  и
и  . На концах отрезка
. На концах отрезка  функция имеет одинаковые знаки
функция имеет одинаковые знаки  , поэтому этот отрезок отбрасываем, а корень уравнения ищем на отрезке
, поэтому этот отрезок отбрасываем, а корень уравнения ищем на отрезке  .
.
2) Находим значение корня во втором приближении.
 . Т.к. длина отрезка
. Т.к. длина отрезка 
 , то точность нахождения корня недостаточна, и потребуется третье приближение. Точка
, то точность нахождения корня недостаточна, и потребуется третье приближение. Точка 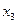 делит отрезок
делит отрезок  на две половины
на две половины  и
и  . На концах отрезка
. На концах отрезка  функция имеет разные знаки
функция имеет разные знаки  , поэтому корень уравнения ищем на этом отрезке
, поэтому корень уравнения ищем на этом отрезке  , а отрезок
, а отрезок  отбрасываем.
отбрасываем.
3) Находим значение корня в третьем приближении.
 . Так как длина отрезка
. Так как длина отрезка 
 , то точность нахождения корня недостаточна, и потребуется четвертое приближение. Точка
, то точность нахождения корня недостаточна, и потребуется четвертое приближение. Точка 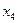 делит отрезок
делит отрезок  на две половины
на две половины  и
и  . На концах отрезка
. На концах отрезка  функция имеет разные знаки
функция имеет разные знаки  , поэтому корень уравнения ищем на этом отрезке
, поэтому корень уравнения ищем на этом отрезке  , а отрезок
, а отрезок  отбрасываем.
отбрасываем.
4) Последующие приближения выполним с помощью компьютерной программы.
Для метода дихотомии:


Результаты расчетов заносим в таблицу 3.1:
 2015-10-22
2015-10-22 550
550








