1. Основные определения. Задача нахождения минимума функции f(x), xÎ[a,b] состоит в нахождении такой точки 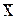 Î[a,b], что
Î[a,b], что
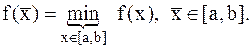 (7.1)
(7.1)
Пусть задана функция f(x) на отрезке [a,b]. Точка 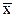 Î[a,b] называется точкой глобального минимума, если для всех xÎ[a,b] выполняется условие:
Î[a,b] называется точкой глобального минимума, если для всех xÎ[a,b] выполняется условие:
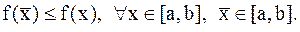 (7.2)
(7.2)
Точка 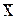 называется точкой локального минимума, если существует d - окрестность этой точки, что выполняется условие:
называется точкой локального минимума, если существует d - окрестность этой точки, что выполняется условие:
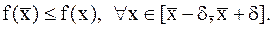 (7.3)
(7.3)
Если 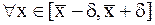 и выполняется условие
и выполняется условие 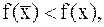 то говорят, что
то говорят, что 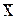 является точкой строгого локального минимума.
является точкой строгого локального минимума.
Унимодальные функции. Если на отрезке [a,b] определена функция f(x) с одной точкой локального минимума 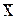 и при этом для всех
и при этом для всех 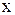 <
< 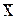 функция строго убывает,
функция строго убывает, 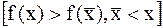 , а для всех
, а для всех 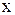 >
> 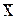 функция строго возрастает
функция строго возрастает 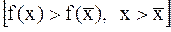 , то такая функция называется унимодальной.
, то такая функция называется унимодальной.
Этапы поиска минимума. Так же, как и в задаче поиска корня, задача поиска минимума разделяется на два этапа: этап локализации и этап итерационного уточнения. На этапе локализации выделяется отрезок минимальной длины, содержащий одну точку локального минимума, на котором функция является унимодальной. На втором этапе используется один из методов поиска точки минимума.
2. Методы прямого поиска:
а) оптимальный пассивный поиск. На отрезке [a,b] задается последовательность точек x0,x1,...,xn, таких, что xk=x0+kh, k=1,...,n; x0=a, xn=b. В этих точках вычисляется значение функции f(xk). За точку минимума 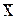 принимается та точка xk, для которой выполняется соотношение:
принимается та точка xk, для которой выполняется соотношение: 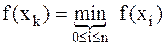 . Следовательно:
. Следовательно: 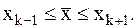 Отсюда предельная относительная погрещность равна
Отсюда предельная относительная погрещность равна 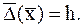
б) метод деления отрезка пополам. На отрезке локализации 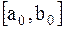 выбирается две точки:
выбирается две точки: 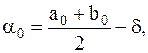
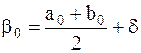 (обычно
(обычно 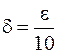 , где e-заданная точностья)и вычисляются значения
, где e-заданная точностья)и вычисляются значения 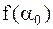 и
и 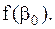 Если
Если 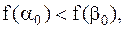 то точка минимума находится на отрезке
то точка минимума находится на отрезке 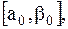 если
если 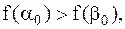 то точка минимума находится на отрезке
то точка минимума находится на отрезке 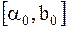 , т.к. функция является унимодальной. Отрезок с точкой минимума принимается за новый отрезок локализации
, т.к. функция является унимодальной. Отрезок с точкой минимума принимается за новый отрезок локализации 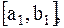 на котором опять выбираются две точки и т.д., до отрезка
на котором опять выбираются две точки и т.д., до отрезка 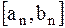 длина которого
длина которого 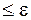 . После этого полагаем
. После этого полагаем 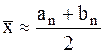 . Следовательно, для абсолютной предельной погрешности нахождения минимума можем записать:
. Следовательно, для абсолютной предельной погрешности нахождения минимума можем записать: 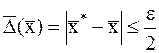 .
.
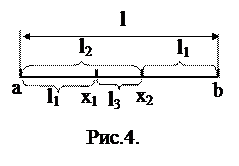 в) метод золотого сечения. Золотым сечением отрезка называется деление отрезка на две части, так что отношение длины всего отрезка к длине большей части равно отношению большей части lк длине меньшей (принцип подобия):
в) метод золотого сечения. Золотым сечением отрезка называется деление отрезка на две части, так что отношение длины всего отрезка к длине большей части равно отношению большей части lк длине меньшей (принцип подобия): 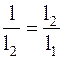 . (Рис.4). Золотое сечение отрезка
. (Рис.4). Золотое сечение отрезка  можно произвести двумя симметрично расположенными двумя точками:
можно произвести двумя симметрично расположенными двумя точками:
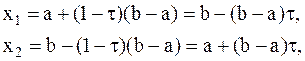 (7.4)
(7.4)
где 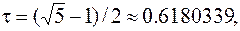
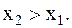
Сечение называется золотым, потому, что точка x1 в свою очередь производит золотое сечение отрезка [a,x2], а точка x2-золотое сечение отрезка [x1,b].
В методе золотого сечения отрезок локализации 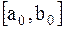 делится золотым сечением на три части двумя точками x1 и x2. Вычисляются значения
делится золотым сечением на три части двумя точками x1 и x2. Вычисляются значения 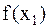 и
и 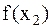 . Если
. Если 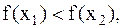 то точка минимума находится на отрезке
то точка минимума находится на отрезке 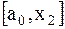 , если
, если 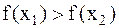 , то точка минимума находится на отрезке
, то точка минимума находится на отрезке 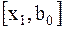 , т.к. функция является унимодальной. Отрезок с точкой минимума принимается за новый отрезок локализации
, т.к. функция является унимодальной. Отрезок с точкой минимума принимается за новый отрезок локализации 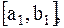 и т.д. до отрезка
и т.д. до отрезка 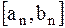 , длина которого
, длина которого 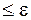 . Полагаем
. Полагаем 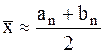 . Следовательно:
. Следовательно: 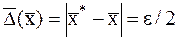 .
.
Так как на каждом последующем шаге, на отрезке локализации выбираются две точки по золотому сечению, то одна из точек уже известна из предыдущего шага, а также известно значение функции в этой точке. Поэтому на каждом шаге необходимо вычислять значение функции только в одной новой точке, в отличие от метода деления отрезка попалам, где необходимо вычислять значение в двух новых точках.
Варианты задания №10
Найти точку минимума функции f(x) с точностью 0,1 указанным методом: а-оптимальн-пассивный поиск, б-метод деления отрезка пополам, в-метод золотого сечения.
1. 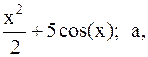 2.
2. 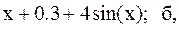
3. 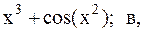 4.
4. 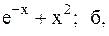
5. 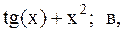 6.
6. 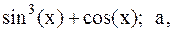
7. 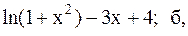 8.
8. 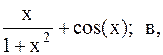
9. 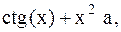 10.
10. 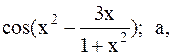
11. 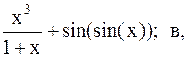 12.
12. 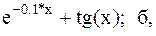
13. 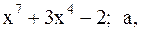 14.
14. 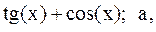
15. 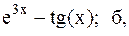 16.
16. 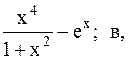
17. 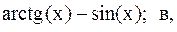 18.
18. 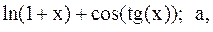
19. 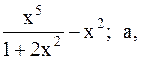 20.
20. 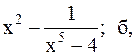
21. 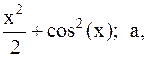 22.
22. 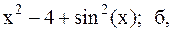
23. 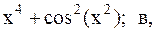 24.
24. 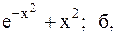
25. 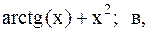 26.
26. 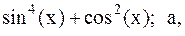
27. 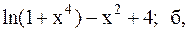 28.
28. 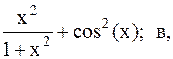
29. 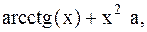 30.
30. 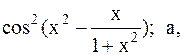
31. 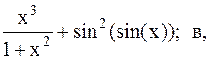 32.
32. 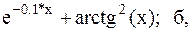
33. 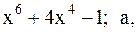 34.
34. 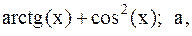
35. 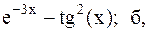 36.
36. 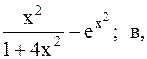
37. 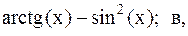 38.
38. 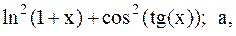
39. 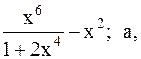 40.
40. 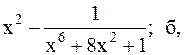
 2015-03-22
2015-03-22 2103
2103
