дифференциальных уравнений на ЭВМ
Система дифференциальных уравнений, которыми описывается состояние любой электрической цепи, может быть решена методом численного интегрирования на ЭВМ (метод последовательных интервалов или метод Эйлера).
Сущность метода состоит в том, что исследуемый промежуток времени Т (при расчете переходных процессов, это Т п - продолжительность переходного процесса) разбивается на большое число N элементарных отрезков времени 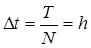 , которые называются шагом интегрирования.
, которые называются шагом интегрирования.
В дифференциальных уравнениях дифференциалы функций заменяются их конечными приращениями, а производные функций - отношениями приращений:
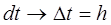
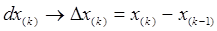
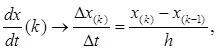 откуда следует:
откуда следует:
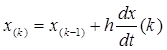
На каждом шаге интегрирования решается система дифференциальных уравнений, в результате решения определяются численные значения производных и самих функций. В качестве исходных данных для их определения используются значения этих же функций на предыдущем шаге, а на начальном 1-ом шаге – их значения в момент коммутации при t =0, т.е. начальные условия. В результате расчета для функций и их производных составляются массивы их значений в исследуемом интервале времени Т, которые после завершения цикла подвергаются соответствующей математической обработке, а именно: строятся графические диаграммы функций, составляются необходимые таблицы, исследуются функции на наличие максимумов и минимумов, устанавливается продолжительность переходного процесса и его характер, и т.д.
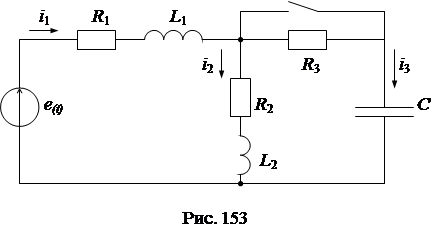
Пример. Рассчитать переходный процесс в схеме рис. 153 с заданными параметрами элементов: 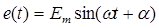 , R 1, R 2, R 3, L 1, L 2, С.
, R 1, R 2, R 3, L 1, L 2, С.
 |
Путем расчета схемы в установившемся режиме до коммутации определяются независимые начальные условия 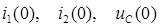 .
.
По законам Кирхгофа для схемы после коммутации составляется система дифференциальных уравнений:
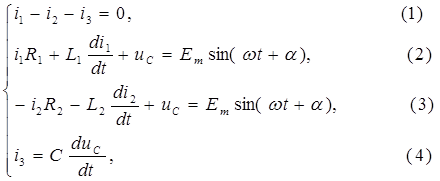
Выбирается шаг интегрирования h (например, из расчета N =1000 шагов на период Т =0,02 с переменного тока, тогда h=Т/ N =2·10-5 с).
Составляется алгоритм вычислений для произвольного к -го шага:
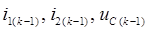 - исходные данные,
- исходные данные,
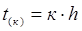 - текущее время,
- текущее время,
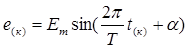 ,
,
из (1) 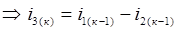 ,
,
из (2) 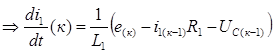 ,
,
из (3) 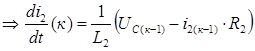 ,
,
из (4) 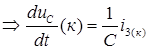 ,
,
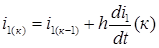 ,
,
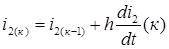 ,
,
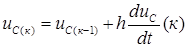 .
.
Далее следуют вычисления по тому же алгоритму для (к +1)-го шага и т. д.
В соответствии с составленным алгоритмом на любом языке составляется программа вычислений на ЭВМ, что представляет собой несложную инженерную задачу.
В настоящее время метод численного интегрирования является наиболее универсальным и наиболее простым методом расчета переходных процессов в электрических цепях. Достоинствами метода являются:
1. Метод численного интегрирования одинаково просто может применяться для расчета переходных процессов в электрических цепях любой сложности, содержащих любое число независимых накопителей энергии L и C. В то же время в классическом и операторном методах с увеличением числа независимых накопителей энергии (и соответственно порядка дифференциального уравнения) значительно возрастают математические сложности, что практически не позволяет применять эти методы для решения дифференциальных уравнений выше 2-го порядка.
2. Метод численного интегрирования позволяет сравнительно просто выполнить математический анализ решения для искомой функции и получить выводы, необходимые для инженерной практики, а именно: определить характер и продолжительность переходного процесса, определить максимальные значения функции и т.д.
К недостаткам метода следует отнести необходимость составления индивидуальной расчетной программы для каждой конкретной задачи и решение ее на ЭВМ, что сегодня уже посильно каждому инженеру.
21. Расчет переходных процессов методом переменных состояния
Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.
В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:
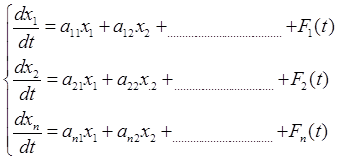
Та же система уравнений в матричной форме:
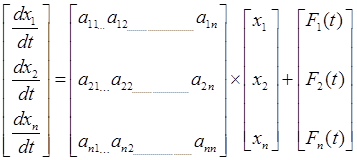
или в обобщённой матричной форме:
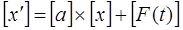
Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к -го шага:
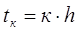
Значения производных на к -ом шаге:
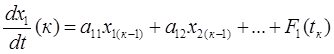
…………………………………………………
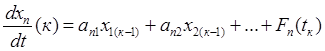
Значения переменных на к -ом шаге:
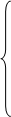
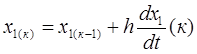
…………………………….
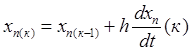
Для определения значений переменных и их производных на 1-м шаге интегрирования используются их значения на момент t =0, т.е. их начальные условия 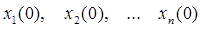 .
.
Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются ''лишние'' переменные, имеющие зависимые начальные условия, и оставляют переменные 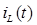 и
и 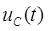 , которые не изменяются скачком и имеют независимые начальные условия
, которые не изменяются скачком и имеют независимые начальные условия 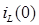 ,
, 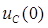 ; б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
; б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.
В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений 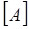 и
и 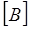 .
.
Последовательность расчета переходного процесса методом переменных состояния выглядит так:
1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия 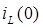 и
и 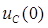 .
.
2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.
3. Методом исключения ''лишних'' переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.
4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.
5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы 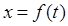 или в виде таблицы координат функций для заданных моментов времени.
или в виде таблицы координат функций для заданных моментов времени.
Пример. Для схемы рис. 154 с заданными параметрами элементов 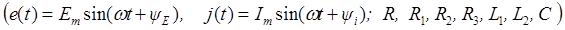 выполнить расчет переходного процесса и определить функцию
выполнить расчет переходного процесса и определить функцию 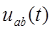 .
.
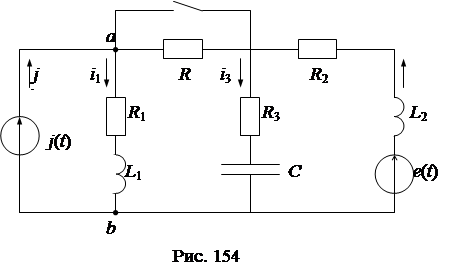 |
1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия 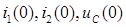 .
.
2. Составляется система дифференциальных уравнений по законам Кирхгофа:
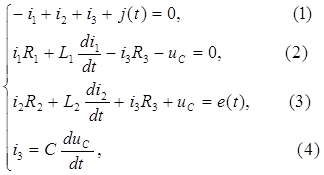
3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.
Для этой цели из (1) выражаем 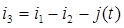 и делаем подстановку в (2) и (3), а из (4) делаем подстановку в (1). Тогда получим:
и делаем подстановку в (2) и (3), а из (4) делаем подстановку в (1). Тогда получим:
из (2) 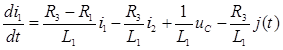
из (3) 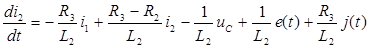
из (1) 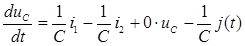
Введем обозначения: i 2 =x 1; i 2 =x 2; uC=x 3. Подсчитаем значения отдельных коэффициентов.
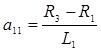 ;
; 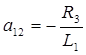 ;
; 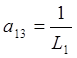
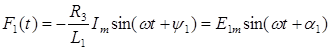 , и т.д.
, и т.д.
Составляем матрицы коэффициентов:
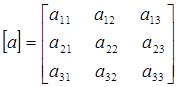 ;
; 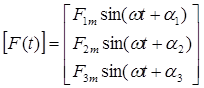
В качестве исследуемого промежутка времени выбираем период переменного тока 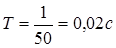 . Число шагов интегрирования принимаем N =1000.
. Число шагов интегрирования принимаем N =1000.
Вводим исходные данные в ЭВМ и выполняем расчет.
В качестве выходной функции принимаем:
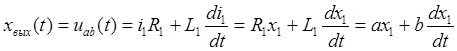 .
.
Для выходной функции  строим графическую диаграмму в интервале периода Т.
строим графическую диаграмму в интервале периода Т.
Т. Четырехполюсники и фильтры
1. Уравнения четырехполюсника
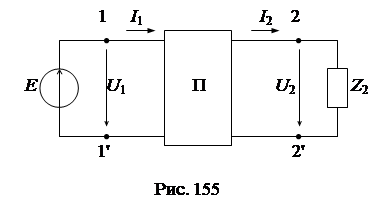
Четырехполюсником называется часть электрической цепи или схемы, содержащая два входных вывода (полюса) для подключения источника энергии и два выходных вывода для подключения нагрузки. К четырехполюсникам можно отнести различные по назначению технические устройства: двухпроводную линию, двухобмоточный трансформатор, фильтры частот, усилители сигналов и др.
Теория четырехполюсников устанавливает связь между режимными параметрами на входе (U 1, I 1) и режимными параметрами на его выходе (U 2, I 2), при этом процессы, происходящие внутри четырехполюсника, не рассматриваются. Таким образом, единая теория четырехполюсника позволяет анализировать различные по структуре и назначению электрические цепи, которые могут быть отнесены к классу четырехполюсников.
Если четырехполюсник не содержит внутри себя источников энергии, то он называется пассивным (обозначается буквой П), если внутри четырехполюсника имеются источники, то он называется активным (обозначается буквой А).
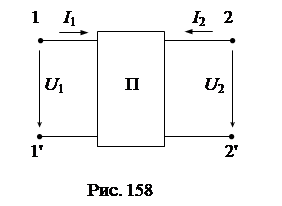
В настоящей главе анализируются пассивные линейные четырехполюсники. На электрических схемах четырехполюсники условно обозначаются прямоугольником с двумя парами выводов: 1 и 1' - входные выводы, 2 и 2' - выходные выводы (рис. 1). Соответственно напряжение и ток на входе индексируются цифрой 1 (U 1, I 1), а на выходе - цифрой 2 (U 2, I 2).
 |
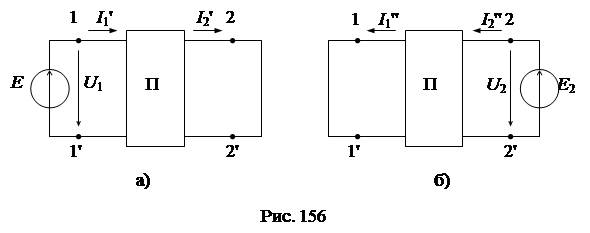
Установим связь между параметрами режима входа (U 1, I 1) и выхода (U 2, I 2). Для этой цели согласно теореме о компенсации заменим нагрузку Z 2 источником ЭДС Е 2 = U 2 = I 2 Z 2 и найдем токи по методу наложения от каждого источника в отдельности (рис. 156а, б):
 |
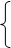
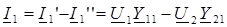
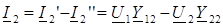 ,
,
где Y 11, Y 22 – входные проводимости входа и выхода, Y 12 = Y 21 – взаимная проводимость между входом и выходом.
Выразим из полученных уравнений режимные параметры на входе:
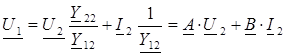
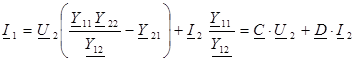 ,
,
где 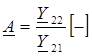 ;
; 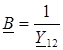 [Ом];
[Ом]; 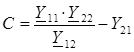 [См];
[См]; 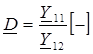 – комплексные коэффициенты четырехполюсника.
– комплексные коэффициенты четырехполюсника.
С учетом принятых обозначений система основных уравнений четырехполюсника получит вид:
| |||
| |||
Уравнения четырехполюсника часто записывают в матричной форме:
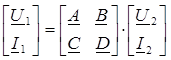 или
или 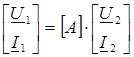 ,
,
где 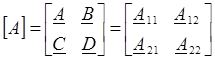 - матрица коэффициентов формы А.
- матрица коэффициентов формы А.
Выразим соотношение между коэффициентами четырехполюсника:
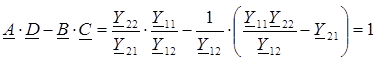
A · D - B · C =1 – уравнение связи между коэффициентами. Уравнение связи показывает, что независимыми являются только три из четырех коэффициентов четырехполюсника.
Поменяем местами в схеме рис. 155 источник и приемник энергии. В новой схеме рис. 157 направления токов изменятся на противоположные.
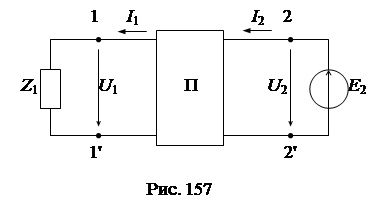 |
Уравнения четырехполюсника с учетом изменения направлений токов примут вид:
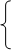
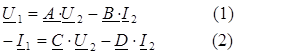
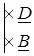
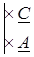
Преобразуем полученную систему уравнений следующим образом. Умножим члены уравнения (1) на D, члены уравнения (2) на В и вычтем почленно из 1-го уравнения 2-ое. В результате получим:
D · U 1 + B · I 1 = (A · D - B · C)· U 2 + (B · D - B · D)· I 2 = U 2.
Умножим члены уравнения (1) на С, члены уравнения (2) на А и вычтем из 1-го уравнения 2-ое. В результате получим:
C · U 1 + A · I 1 = (A · C - A · C)· U 2 + (A · D - B · C)· I 2 = I 2
Новая система уравнений четырехполюсника получила название формы В:
| |||
| |||
Четырехполюсник называется симметричным, если перемена местами входных и выходных выводов не влияет на режим остальной цепи, частью которой является четырёхполюсник. Для симметричного четырёхполюсника А = D и A 2 - B · C =1.
Кроме названных форм уравнений четырехполюсника А и В применяются на практике еще четыре формы, а именно формы Z, Y, H и G. Структура этих уравнений приведена ниже:
| |||||||
| |||||||
| |||||||
| |||||||
| |||||||
| |||||||
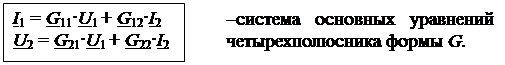 |
Для уравнений формы Z, Y, H и G принята следующая ориентация токов и напряжений относительно выводов четырехполюсника (рис.158).
 |
Соотношения между коэффициентами четырехполюсника различных форм приводятся в справочной литературе, однако их нетрудно получить, выполнив преобразование одной формы уравнений в другую. Например, пусть заданы коэффициенты формы А (А, В, С, D) и требуется определить коэффициенты формы Z (Z 11, Z 12, Z 21, Z 22). Для этого в уравнениях формы A изменим знак тока I 2 и решим их относительно переменных U 1 и U 2:
U 1 = A · U 2 - B · I 2 (1)
I 1 = C · U 2 - D · I 2 (2)
Из (2) следует: 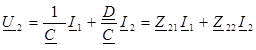 .
.
Из (1) следует: 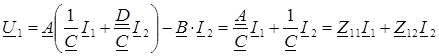 .
.
Сравнивая полученные выражения с уравнениями четырехполюсника формы Z, находим соотношения между коэффициентами двух форм:
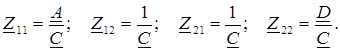
 2014-02-09
2014-02-09 4273
4273
