Сложение скоростей в теории относительности

Пусть некоторая точка М движется относительно системы 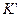вдоль оси со скоростью . Скорость её относительно неподвижной системы 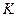будет:

, (5.6)

Координата этой точки определится из формул (5.3):

, откуда , (5.7)

Аналогично определяем :

, (5.8)

Подставляя (5.7) и (5.8) в (5.6) и учитывая, что , получаем:

, (5.9)

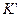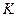Эта формула выражает релятивистский закон сложения ско­ростей. Сравнивая (5.9) с (5.2), видно, что при малых скорос­тях теорема сложения скоростей Галилея остаётся вер­ной. Из формулы (5.9) следует предельный характер скорости света. Действительно, если относительно послать световой импульс со скоростью , то относительно получим:

,

т.е. в системе 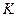скорость светового импульса тоже равна 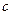. Найдем другие составляющие скорости и .

Так как , то:

, (5.10)

Из формулы (5.3) находим:

Подставляя это в (5.10), получим:

(5.11)