Модели, приводящие к необходимости численного дифференцирования и интегрирования функций

Одномерное волновое уравнение — однородное линейное уравнение в частных производных гиперболического типа второго порядка с постоянными коэффициентами, описывает колебание струны, если 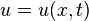— отклонение струны в точке с координатой x в момент времени t, а параметр a задаёт свойства струны:

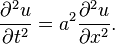
Уравнение Лапласа в двумерном пространстве — однородное линейное диффур в частных производных 2-го порядка эллиптического типа с постоянными коэффициентами, возникающее во многих физических задачах механики, теплопроводности, электростатики, гидравлики:

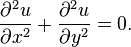
Уравнение Кортевега-де Фриза, нелинейное диффур в частных производных 3-го порядка, описывающее стационарные нелинейные волны, в т ч солитоны:

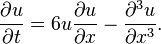
Задача Абеля (1823) обобщение задачи о таутохроне

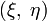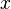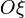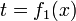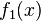Формулировка задачи (у Абеля): материальная точка под действием силы тяжести движется в вертикальной плоскости по некоторой кривой. Требуется определить эту кривую так, чтобы мат точка, начав свое движение без начальной скорости в точке кривой с ординатой , достигла оси за время , где — заданная функция.

где 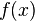— заданная функция, а 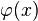— искомая. Это уравнение есть частный случай линейного интегрального уравнения Вольтерра 1-го рода. Ур Абеля интересно тем, что к нему непосредственно приводит постановка той или иной конкретной задачи механики или физики (минуя диффур).

Если обозначить угол между касательной к траектории и осью 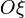как 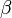и применить законы Ньютона, можно прийти к следующему уравнению:

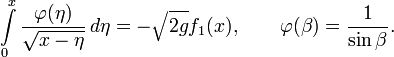
Модель Мальтуса: скорость роста пропорциональна текущему размеру популяции:

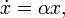
где α - некоторый параметр, определяемый разностью между рождаемостью и смертностью. Решение: 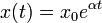. Если рождаемость > смертности (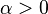), размер популяции неограниченно и быстро возрастает. Реально такого нет (ограниченность ресурсов). Уточнение модели Мальтуса: логистическая модель: диффурФерхюльста:

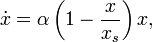
где 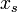— «равновесный» размер популяции (рождаемость компенсируется смертностью). Размер популяции в такой модели стремится к равновесному значению 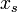, причем такое поведение структурно устойчиво.

Система хищник-жертва: на нек-ой территории обитают 2 вида жив-ых: кролики (пит растениями) и лисы (пит кроликами). Число кроликов 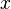, число лис 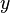. Из модели Мальтуса с поправками (поедание кроликов лисами): модель Лотки --Вольтерра

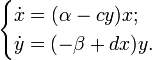
Эта система имеет равновесное состояние, когда число кроликов и лисconst. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Это поведение не является структурно устойчивым: малое изменение модели (учитывающее ограниченность ресурсов, необходимых кроликам) может привести к кач-му изменению поведения (равновесное состояние может стать устойчивым, и колебания численности будут затухать). Или: любое малое отклонение от положения равн-ия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. Реализацию сценариев модель не рассм.