Модели, описываемые обыкновенными дифференциальными уравнениями, методы решения

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ОДУ) — это уравнения, зависящие от одной независимой переменной; они имеют вид

или

где — неизвестная функция, зависящая от независимой переменной x Число - порядок диффур.

Наиболее практважные:диффур1-го и 2-го порядка.

ПРИМЕР

1 из простейших применений диффур— решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения:

по2-ому закону Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид . Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.

Дифференциальное уравнение , вместе с начальным условием , задаёт экспоненту: .

Если 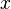обозначает время, то эта функция описывает, например, рост популяции в условиях неограниченности ресурсов, а также и многое другое.

Решение диффур , правая часть которого не зависит от неизвестной функции, является неопределённый интеграл:

, где 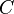— произвольная константа.