Элементы теории двойственности

Двойственная задача (5) может быть получена и абстрактно, исходя из общей теории двойственности, из которой следует, что всякой задаче на максимизацию с ограничениями в форме неравенств со знаком “меньше или равно” и расширенной матрицей (4.1) можно сопоставить двойственную к ней задачу на минимизацию с ограничениями в форме неравенств со знаком “больше или равно” и расширенной матрицей, транспонированной к (4.1). Вообще говоря, теория двойственности не определяет как исходную именно задачу (4). В этой теории обе задачи являются двойственными друг к другу. В теории двойственности доказываются следующие свойства (теорема двойственности) задач (4) и (5):

1. Если одна из этих задач имеет конечный оптимальный план, решение, то конечный оптимальный план имеет и двойственная к ней задача, причём значения целевых функций в оптимальных планах обеих задач совпадают.

2. Если задача (4) имеет бесконечный оптимальный план (целевая функция не ограничена сверху в МДП), то МДП задачи (5) - это пустое множество (задача допустимых планов не имеет). И наоборот, если задача (5) имеет бесконечный оптимальный план (целевая функция не ограничена снизу в МДП), то МДП задачи (4) - это пустое множество.

Способы решения

Поскольку решения задачи ЛП находятся в вершинах МДП, основным способом решения является метод перебора вершин МДП, который, однако, имеет разные модификации. Среди них следует упомянуть пригодный в любой ситуации метод полного перебора (определение координат всех вершин МДП и вычисление в каждой вершине значения целевой функции с выбором оптимального – наибольшего или наименьшего – значения). Этот метод является самым неэффективным, т.к. число вершин МДП – N - удовлетворяет неравенству: N £ 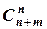, а число сочетаний С – весьма быстро возрастающая функция размерности задачи. Однако задача одномерной оптимизации (n =1) легко разрешима в методе полного перебора, т.к. МДП для неё – отрезок, в одном из двух вершин которого и наблюдается оптимум. При малом (n =2) количестве переменных общей задачи ЛП (4), когда МДП можно изобразить графически на плоскости, применим графический метод поиска решения, имеющий два варианта – градиентный метод и метод линий постоянного уровня, впрочем, чрезвычайно схожих, хоть и получаемых из совершенно различных подходов поиска оптимального решения в общем случае математического программирования. Порядок их следующий: 1) построение МДП; 2) поиск оптимального плана. Пункт 2) в градиентном методе выполняется путём построения вектора градиента целевой функции grad (L(x)) =(c₁,c₂) и выбора вершины МДП, наиболее удалённой (для задачи максимизации) или ближайшей (для задачи минимизации) к началу координат вдоль направления градиента (эти два плана называются опорными). в методе линий постоянного уровня пункт 2) выполняется путём построения линии постоянного уровня целевой функции, во всех точках которой у L(x) наблюдается одинаковое значение L ₀(это прямая с уравнением c₁x₁+c₂x₂=L ₀). Одно из свойств задачи ЛП – параллельность всех её линий постоянного уровня. выбор вершины МДП, являющейся решением, производится при перемещении линии постоянного уровня от начала координат через МДП. Опорными являются первая и последняя вершины, через которые прошла перемещаемая линия. наиболее удалённая от начала координат вершина – решение для задачи максимизации, а ближайшая к нему - решение задачи минимизации. Подробнее см. в примере выполнения задания №2. Вообще говоря, подобная процедура могла бы быть пригодной в случае любой размерности, однако при n =3 грани МДП – плоскости, поверхность постоянного уровня целевой функции также плоскость в трёхмерном пространстве (см. рис. 2). Здесь точки А и В – опорные планы на минимизацию и максимизацию, a и b - поверхности постоянного уровня целевой функции. при большей размерности представить воображаемый вид МДП не возможно в принципе, т.к. грани МДП и поверхность постоянного уровня L(x) – гиперплоскости в n- мерном пространстве. При этом, однако, как было отмечено выше, можно проанализировать задачу (4) с помощью дифференциальных коэффициентов ресурсоотдачи и понизить её размерность. В случае снижения числа не равных нулю переменных до 2-х можно использовать графический метод.

Альтернативным к методам понижения размерности и полного перебора, пригодным при любой размерности задачи методом является симплекс- метод, алгоритм которого будет изложен ниже. Этот метод является частным случаем итеративных методов, смысл которых в последовательном улучшении исходного допустимого решения. В симплекс- методе решения задачи ЛП все промежуточные решения находятся в точках базовых планов – вершинах МДП, сама итеративная процедура состоит в переборе вершин МДП от опорного плана на минимизацию в сторону опорного плана на максимизацию с последовательным гарантированным увеличением (не уменьшением) значения целевой функции в каждой анализируемой точке.